DRL 李宏毅笔记整理

全世界最好的DRL课程笔记整理：Deep Reinforcement Learning, 2018，Hung-yi Lee

数学基础

• 在数学上，表达式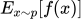表示对随机变量x在概率分布p下的函数f(x)的期望值。具体来说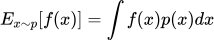，。这里的x~p表示x服从概率分布p，这个期望值表示在x服从p分布的条件下，f(x)的平均值。

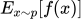• 这个期望值可以近似求解（假如我们不可能列举出所有的x）：

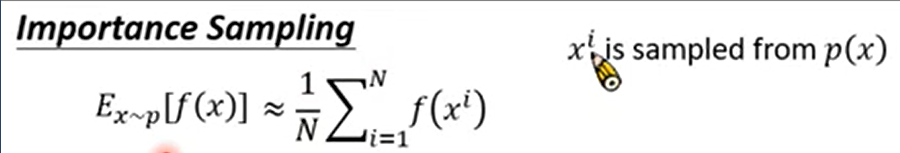
可以根据p(x)这个概率分布中取样一些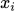，在累加取平均值，近似的模拟期望值。

• 假如x不服从p的概率分布，而是服从另一个概率分布q，可以通过importance sampling的方法来将对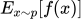的求解问题转化为对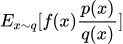的求解问题。

但是p分布和q分布差太多是有问题的。

两个服从于不同分布的随机变量x，他们的期望值（也就是mean）可以是一样的，但是方差是可以不一样的。

举例说明：

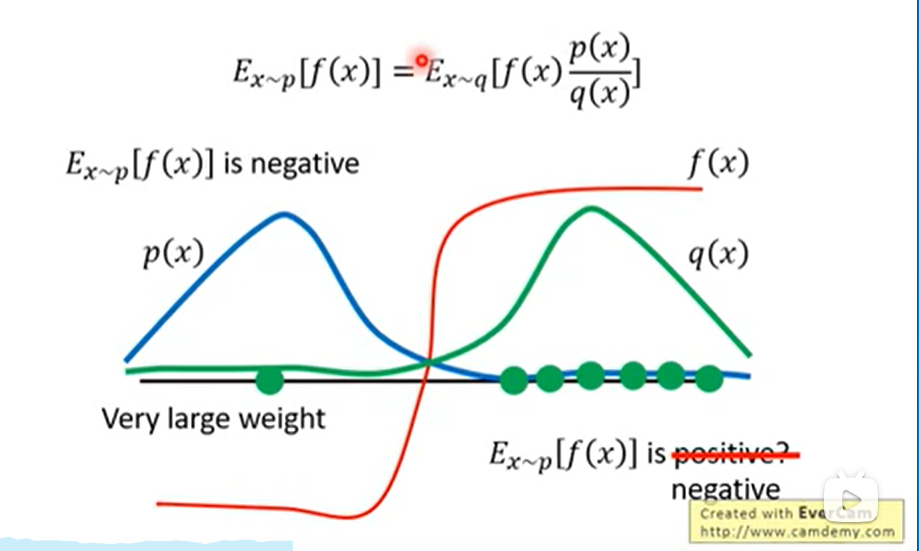
对于上图来说，如果sample的次数不够多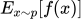，大概率是负的。因为p分布大概率采样到f(x)的左侧。而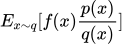大概率会是正的。因为q分布大概率采样到f(x)右侧。

如果采样的次数足够多，例如q分布好不容易采样到左侧，那么f(x)的负值会乘以一个很大的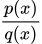项，importance sampling的方差差距就不会那么大了，但是这是做不到的。

• f(x)的梯度计算公式为：

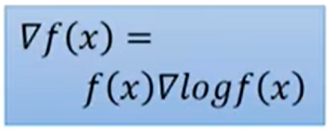
• 熵：

一个概率分布的熵，也就是信息量，可以通过下列公式求得。一个概率分布中熵很大，意味着每个事件都具有相对较高的不确定性，也意味着没有哪个事件的概率特别高，所有事件概率都较为均匀分布。同时，高熵表示该分布中包含更多的信息，也意味着该分布中的事件更为随机，没有明显的模式或者规律。

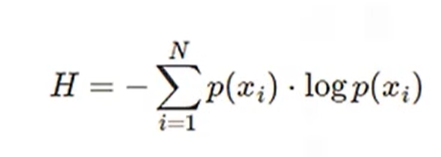
• 香农熵：

在一个系统中，存在多个随机事件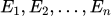，而每个事件出现的概率是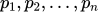，那么这个系统的平均信息量，就是

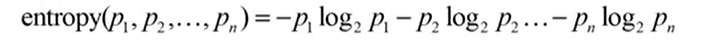
也就是上述的熵的计算公式。底数取2是因为计算机数据是二进制。

• KL散度：

假设现在有一个分布f，他是从真实数据中统计而来：

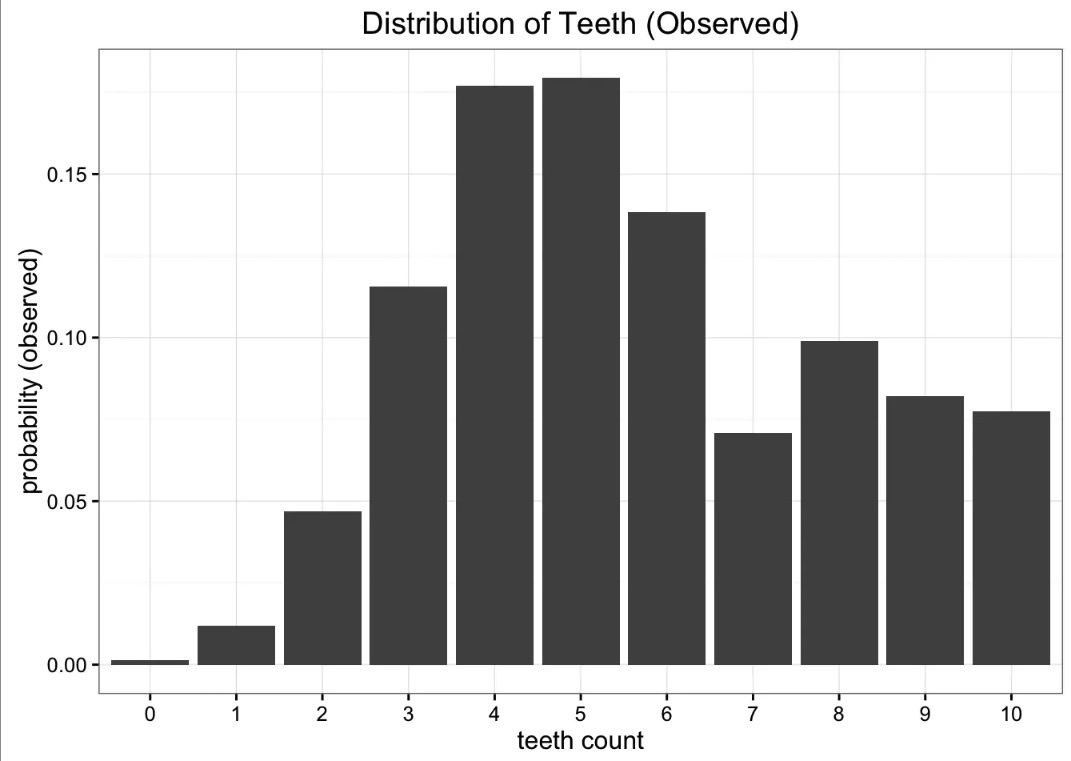
直接描述这个分布太复杂，我们希望能够通过一个近似的，简单的分布来模拟真实分布的表述，例如二项式分布：

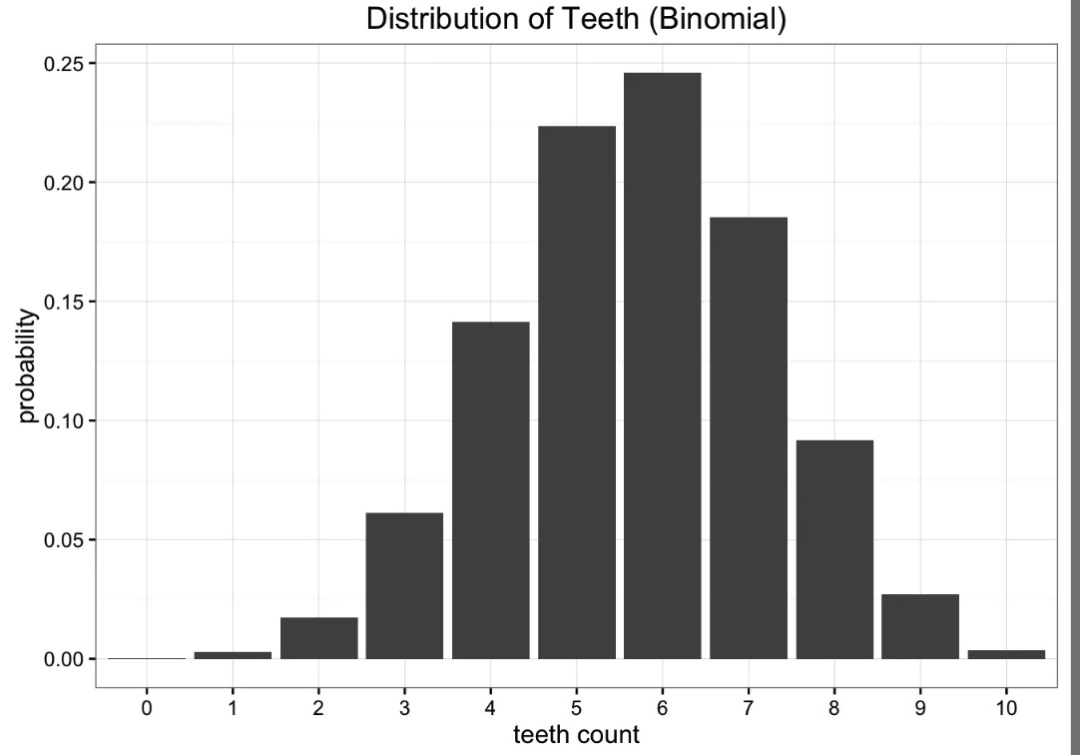
在模拟的过程中，分布的信息会发生丢失。KL散度就是用来描述损失的信息量有多少。

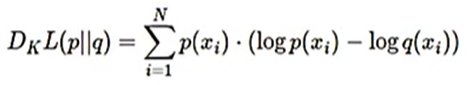
Policy Gradient

• 一个强化学习的组成环境有：Actor，Env，Reward Function

• policy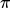是Actor采取的策略。它是一个有着参数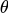的神经网络，输入是环境的观测值，可以是向量或者矩阵，输出是输出层中每个神经元输出的action。

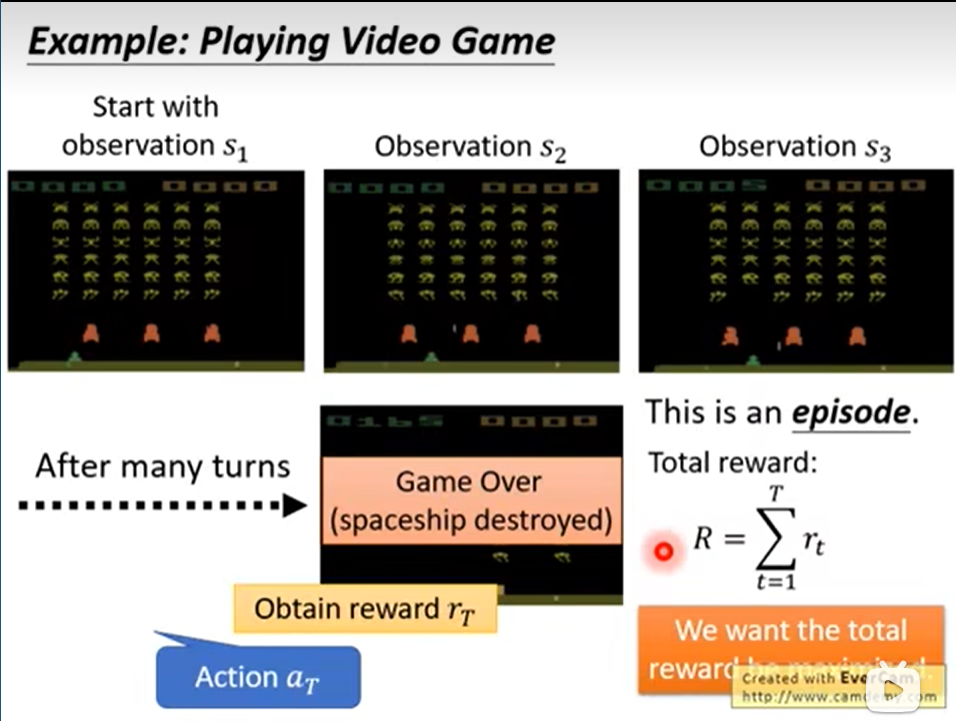
• 在一场游戏中：输入是游戏中每一帧的图片，输出是每一个action对应的几率（分数）。最终选择几率最大的action。

• 一场游戏从头玩到尾叫做一个episode。一个episode中所有的action和state的pair的集合叫做一个trajectory。在这个episode中的Total reward可以是所有执行action后得到的reward的累加：

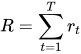
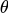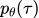• 在参数参数 固定时，agent与环境交互，Trajectory 发生的机率 是：

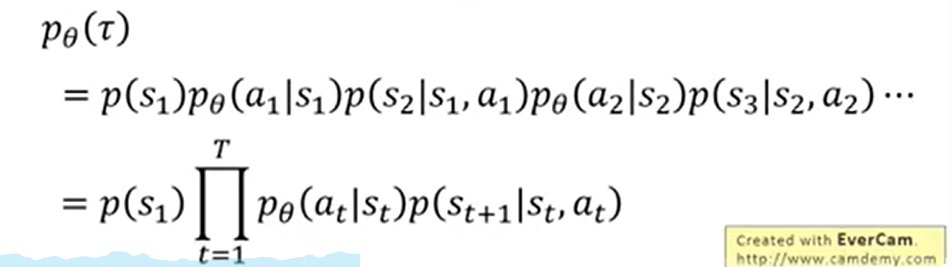
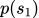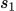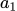• 解析：游戏开始时environment输出的几率乘以policy在时输出的概率...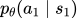

• 在上面的项中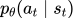，是可以控制的。

• 想要提升一个episode里面的Total reward 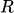。但实际上它是一个random variable。因为environment在给定一个action后，会产生什么样的一个新的observation是具有随机性的。所以只能让Total reward的期望值最大。

• Total reward的期望值计算公式为：

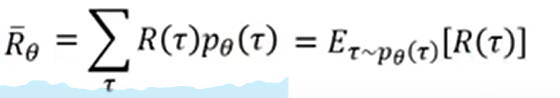
• 把所有的trajectory下得到的total reward乘以他们对应的概率，再整体求和。

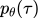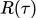• 从这个分布，sample一个trajectory，计算的期望值。

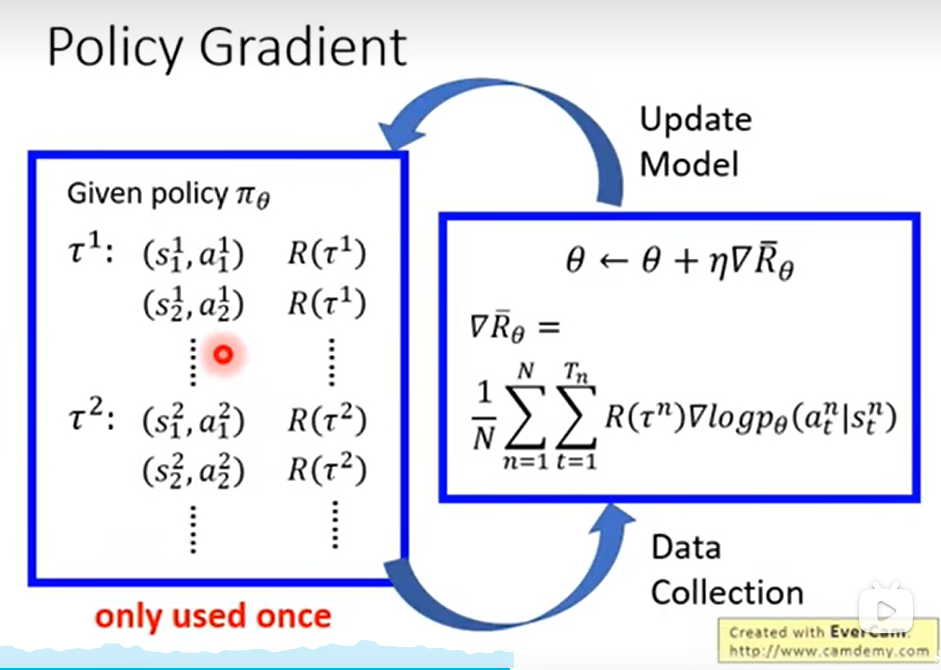
• Total reward的期望值的policy gradient使用了policy ascent，其中R项与policy的参数无关，计算公式为：

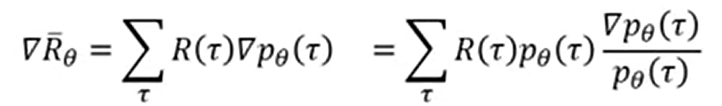
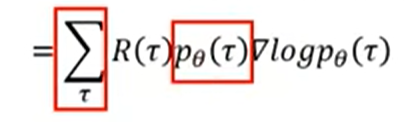
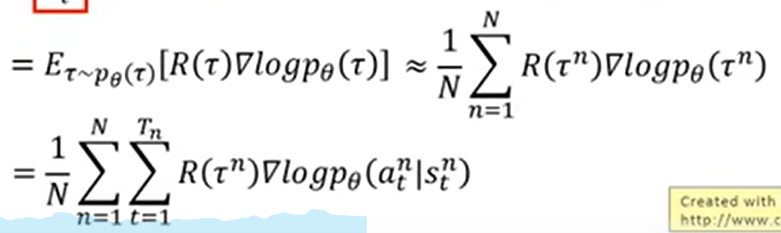
第二行中，由于无法列举出所有的trajectory，因此我们sample出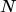笔，来近似的模拟列举出所有的trajectory，每一个trajectory都分别计算，再全加起来取个平均值来近似的模拟。

第三行中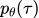， 中只有可控制部分才会用来做policy ascent。

• 在实作中，

  • 首先要收集一大堆trajectory，也就是s和a的pair，然后拿去计算梯度，然后根据学习率更新参数。

• Tip 1：add baseline policy gradient 的公式中，如果在某个state执行一个action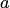导致这个pair所在trajectory的total reward是正的，那么就应该增加这个pair的log probability。反之，reward是负的，那就应该减少log probability。 但是在很多游戏中，reward没有负分，这也就导致R总是正的。进而导致P的上升。 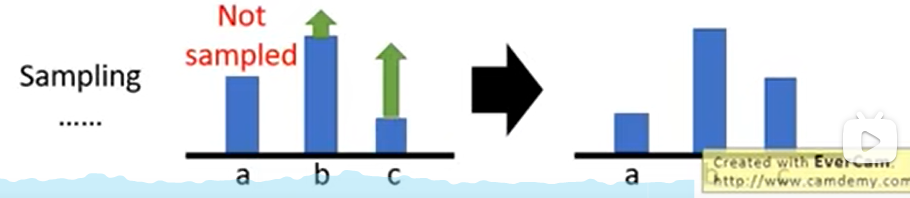假设在上面的例子中，在某一个state下有a，b，c三个action。其中，b和c被sample到了，a没有。由于b和c的reward都是正的，对应的log probability也会上升。由于概率的总和为1，那么a的probability就会下降。但是这并不代表a就不好，a只是没被sample到罢了。

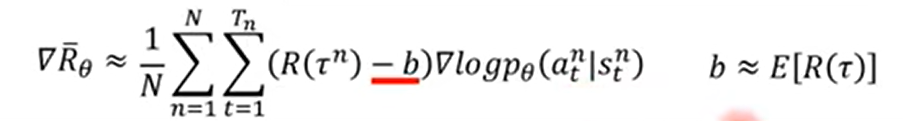通过添加一个base line 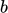来解决这个问题。其中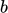，可以是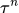的total reward的期望值的平均值。

• Tip 2：应该给每一个action一个合适的credit。 policy gradient 的公式中，每一个action和state的pair的log probability乘以的都是整场游戏的R。也就是说，在一场游戏中，所有的pair的log probability乘以的都是相同的R。这是不公平的。因为一场游戏里的action是有好有坏的。最终的奖励高不代表这个episode中的某一个action好。 解决方案是在计算某一个pair真正的reward时，我们转而计算在执行这个action后，后面累积的reward。同时，对比较未来的reward添加一个discount factor。 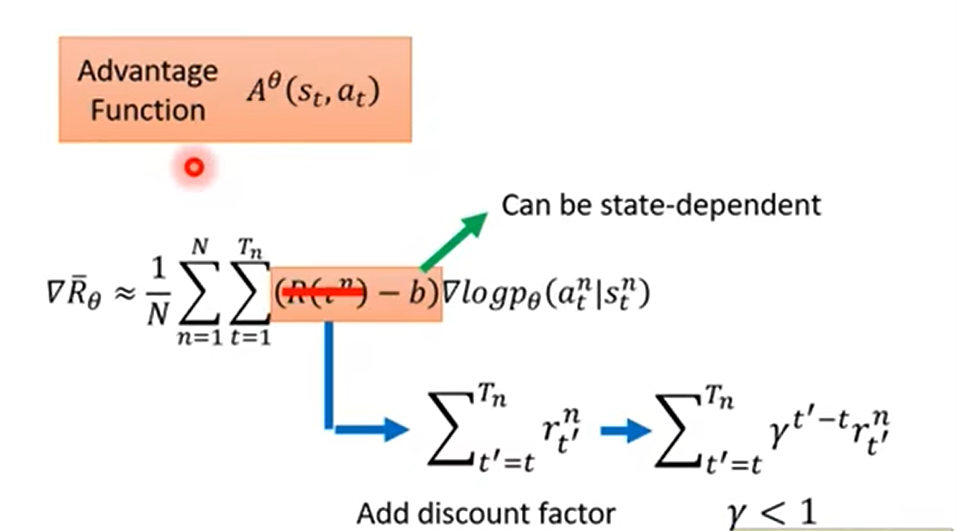Advantage function表明，在给定的state s下，采取action a，有多”好”（即Total reward 是多少）。 注意这里是近似值。是sample了一些trajectory近似出来的值。真正的gradient公式是：

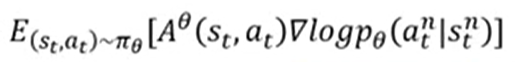
PPO

• on-policy：更新参数的agent和与环境互动的agent是一个agent。

• off-policy：更新参数的agent和与环境互动的agent不是同一个agent

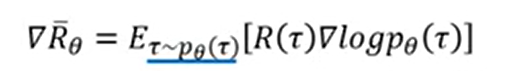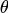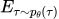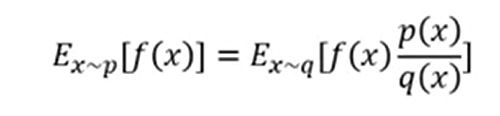• 回顾Policy Gradient公式（注意，这里的公式是简化，不考虑tips的版本）： 从公式里可以看出，on-policy的agent和环境互动后更新完参数 后，的值也就随之变化了。也就是说，sample了一笔trajectory，只能用来更新一组参数。这是比较低效率的。 也就是说，可以使用importance samplling。 也就是：

• 这里要注意的是：

  • 第二行中，从公式的角度上来说，应该是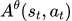。但是其实我们应该算的是真正与环境交互的那个agent的奖励函数。所以替换为是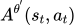。这里替换是因为假设二者差别不大。

  • 第三行中，和之前类似，只考虑概率的可控部分，概率的不可控部分我们假设二者差别不大，消去。

  • 个人认为原ppt错误。n这个项没有意义。

通过蓝框中的公式消去，可得：

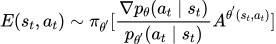
即，我们需要梯度上升的目标函数为：

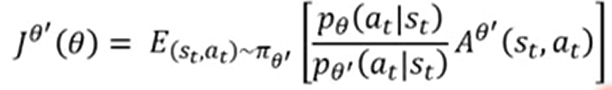
然后，根据前面的推论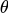，和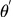之间不能差太多。PPO的做法是在目标函数的基础上加上一个KL散度约束，来确保两个policy之间差不多。 这里的差不多指的是输出的action的分布的距离，而不是policy参数的距离。

• 完整流程为：

超参数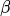的大小要根据KL散度的值和设置的可接受的KL散度的最大值和最小值来进行动态调整。

• PPO2：

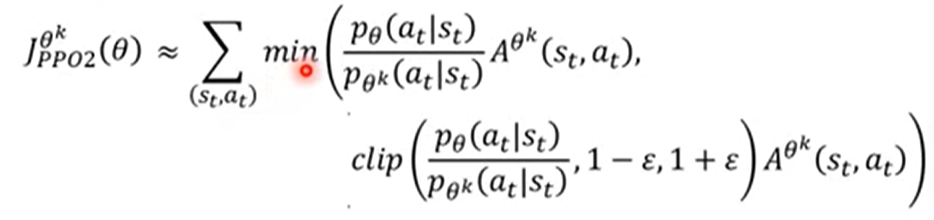
公式解释：

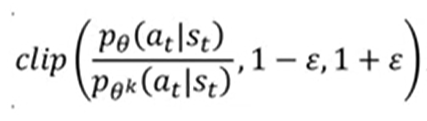
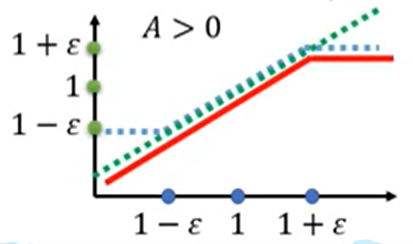
上述函数的图如下所示（蓝色线）：

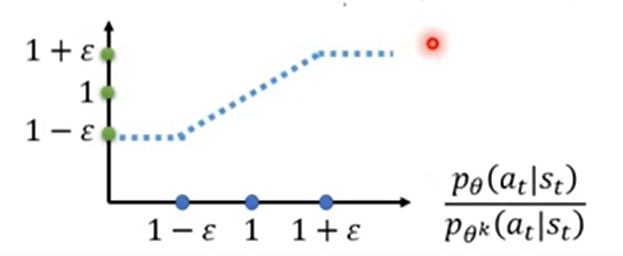
假设下列函数为绿线：

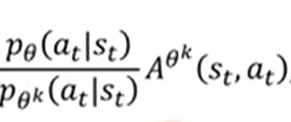
也就是说，整个PPO2的算法本质，就是在绿线和蓝线中间取最小值。

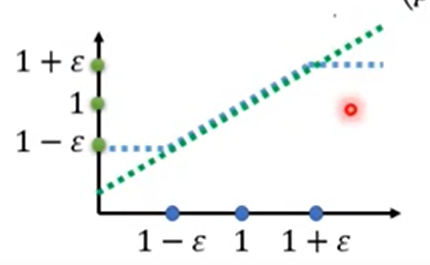
如果A大于0，也就是这个pair所做的事是好的，有利于total reward增加的。那么我们就希望增大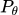的概率，让这个s和a的pair出现的几率越大越好。但是也不能太大，不能和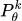差太多。那么取乘在A前面的系数小的，因此在蓝线和绿线之间取最小。

反之，如果A小于0，也就是这个pair所做的事是不好的，不利于total reward增加的。那么我们就希望减小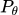的概率，让这个s和a的pair出现的几率越小越好。但是也不能太小，不能和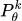差太多。那么取乘在A前面的系数大的，因此在蓝线和绿线之间取最大。

Q learning（Basic idea）

我们learn的是critic，即评价现在actor的行为有多好。

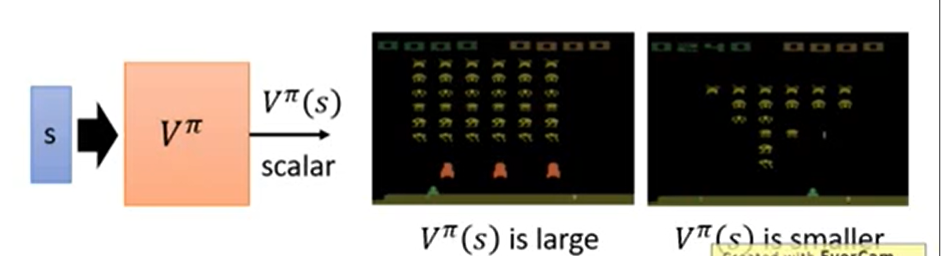
• State value function 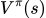的意义是，给定一个state s和一个policy 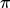，输出的是一个标量scale，即在当前的环境，policy 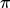玩完这局游戏的预计分数是多少。

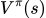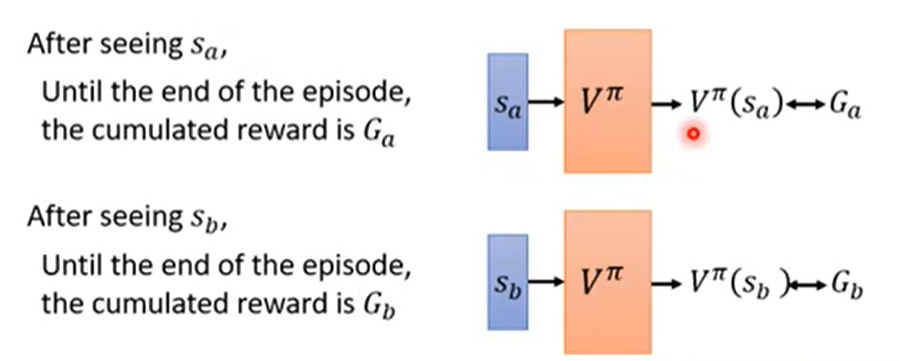
• 衡量的方法有TD和MC。

  • 假设一个actor在state s下玩完整场游戏，得到的累积奖励是G。蒙特卡罗MC法的本质是用一个网络，根据state s来预测一个值，这个值和真值G的loss越小越好。本质是一个回归问题。

• TD时间差分法：MC的方法要把游戏玩完才可以update reward，时间太长了。所以可以使用TD的方法，考虑每一个step之间的差距。假设现在的actor在时间t时环境的状态为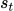，policy输出的action是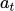，采取action后得到的奖励是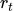。那么这个policy在时间t和时间t+1的累计奖励满足：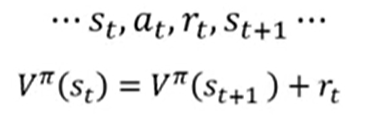

• 那么只需要训练一个网络，做差值回归即可：

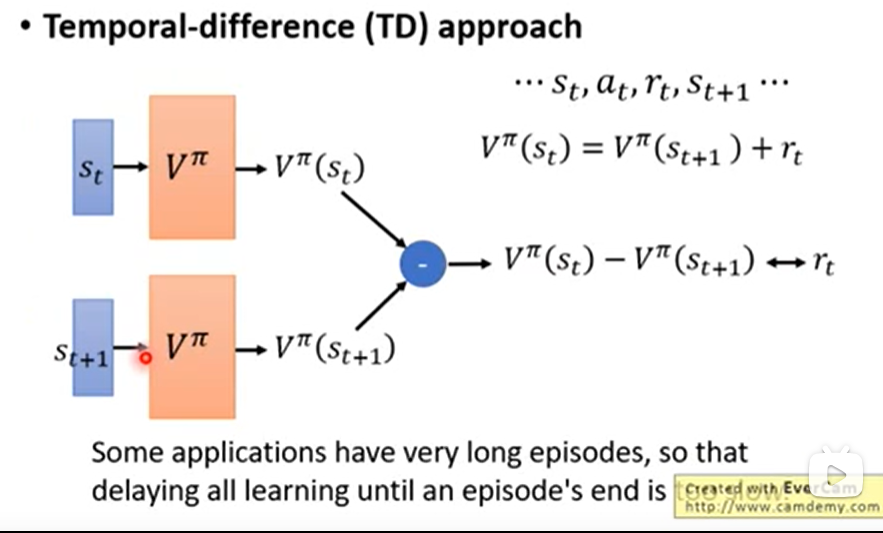
• MC和TD的区别：

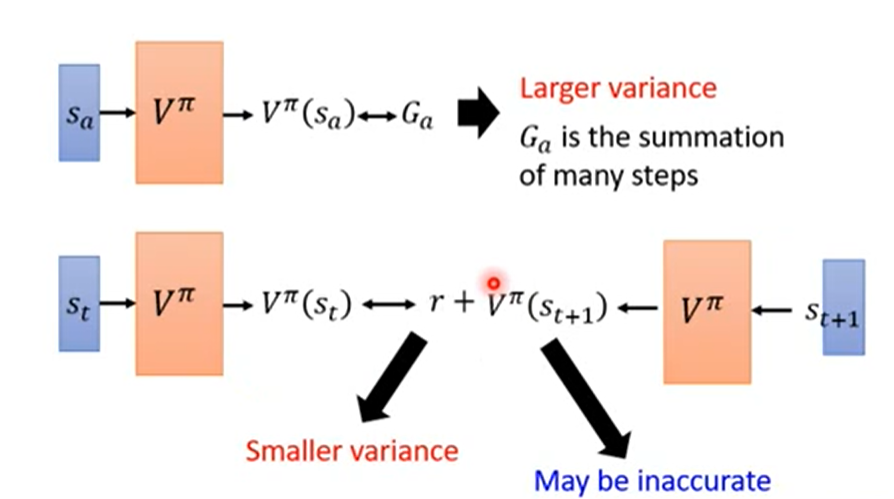
MC更精确，因为TD每一次估计的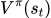和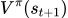都是有误差的。但是MC是一个actor玩完整场游戏，只需要估计一次，所以相对更准。

TD方差小。因为每一step中，即使相同的actor和state，得到的reward r也可能不一样，即r是一个随机变量。MC是很多个r的累积，即不确定性的累积。而TD只考虑不确定性一次。

这里给出”准确”和”方差”的具体描述：

• 偏差：有偏差的估计器不能很好地表示/拟合原始指标。形式上，如果估计量的期望值等于原始度量，则它是无偏的。偏差会导致局部最优解。

• 方差：具有高方差的估计量具有很大的值分布。理想情况下，无偏估计器应该具有低方差，以在输入中始终匹配原始度量。形式上，这与测量任何随机变量的方差相同。方差会导致需要更多样本才能收敛。

• State-action value function 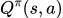描述的意义是：在当前的state s下，actor 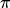强制的执行action a，玩完整场游戏后采取的累积奖励有多大。有两种写法：

  • 给s和a，输出一个scale（a可以是离散的或者是连续的）：

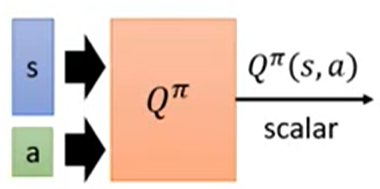
• 给一个s，根据不同的a输出不同的scale（假设a是离散的，可以穷举的）：

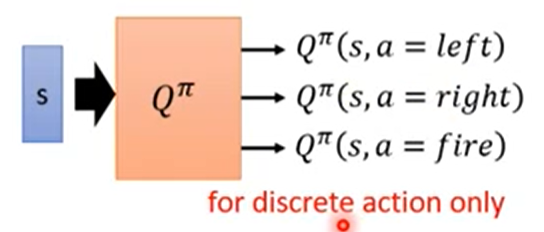
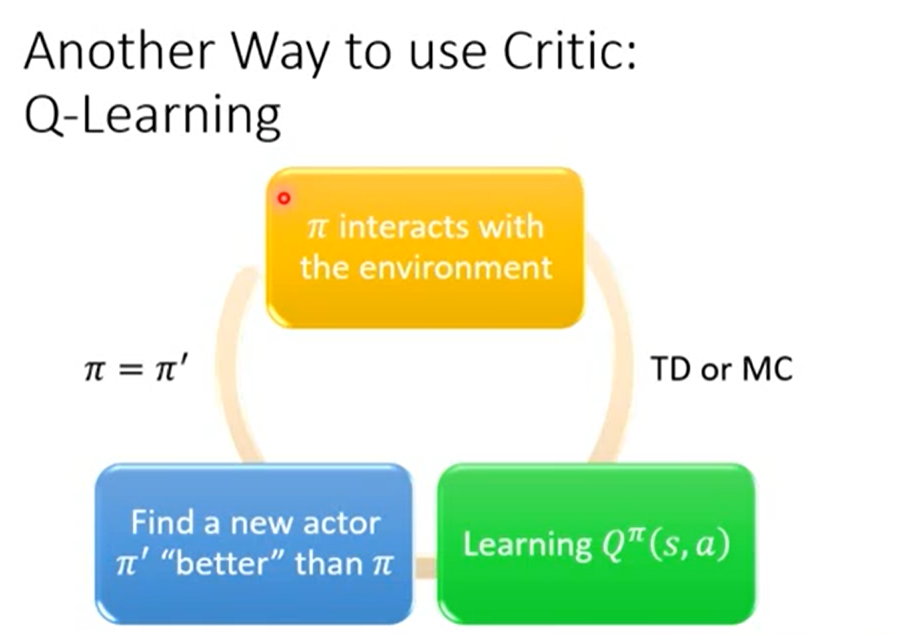
• 使用Q funtion做RL的步骤：

• 也就是说，给定一个Q function，是一定可以找到一个新的actor 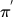，比原来的actor 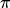要好。这里的好是通过V function定义：

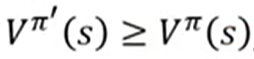
• 如何找这个新的actor 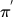呢？公式如下：

• 公式的意义是：

  • 等号右边：让这个actor 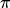和当前的环境s互动，采取能得到的最大的累积奖励的action a。

  • 等号左边：一个策略的映射，表示在当前的state s下，policy 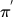采取的action 是什么。

• Q function在learn的时候要有一个target network：

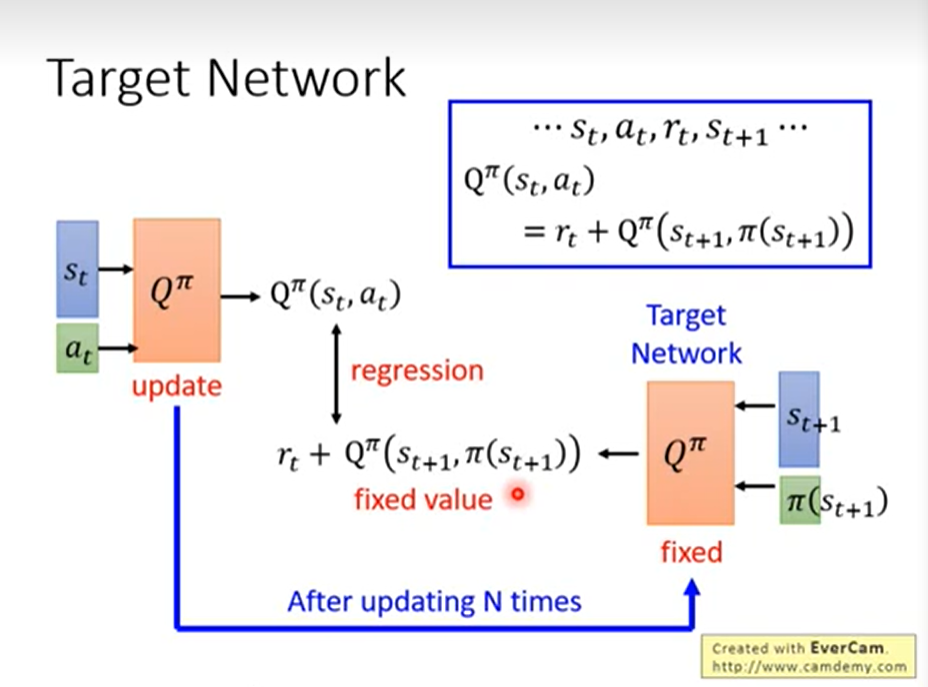
左边和右边的Q都update的话，不太好train，因此右边要固定住。一开始调左边，回归的loss和fixed的网络越接近越好。update几次后把右边的fixed网络替换为左边的update网络。

• 探索问题：Q learning存在探索问题。奖励高的action会总是被sample到，这样就没有探索性了。

• 解决方法有：

  • 贪心Epsilon Greedy:

• boltzmann exploration:

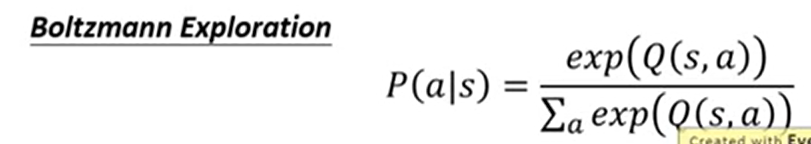
• Replay Buffer：

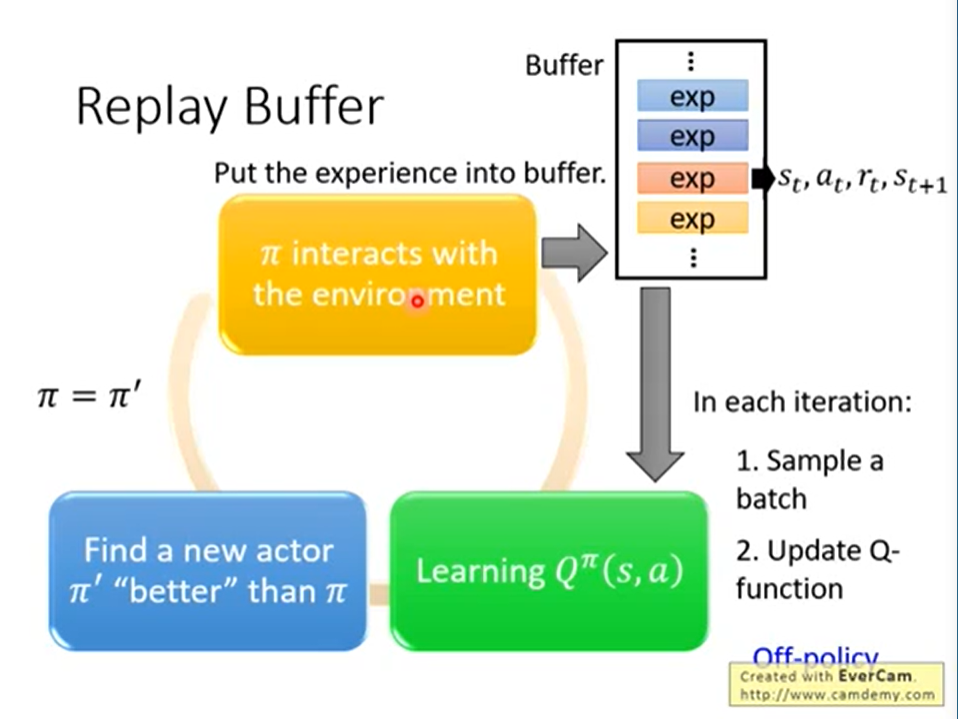
Buffer里面不光有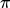和环境互动的pair，还有其他的policy（例如过去的policy交互的pair）。

• 注意这里不要弄混的是，Q learning train的是用来估计值函数的神经网络。而policy gradient更新的是policy的参数。

• 完整的Q learning 算法是：

Q learning（Advanced Tips）

• Q value估计的值是比真实值大的。

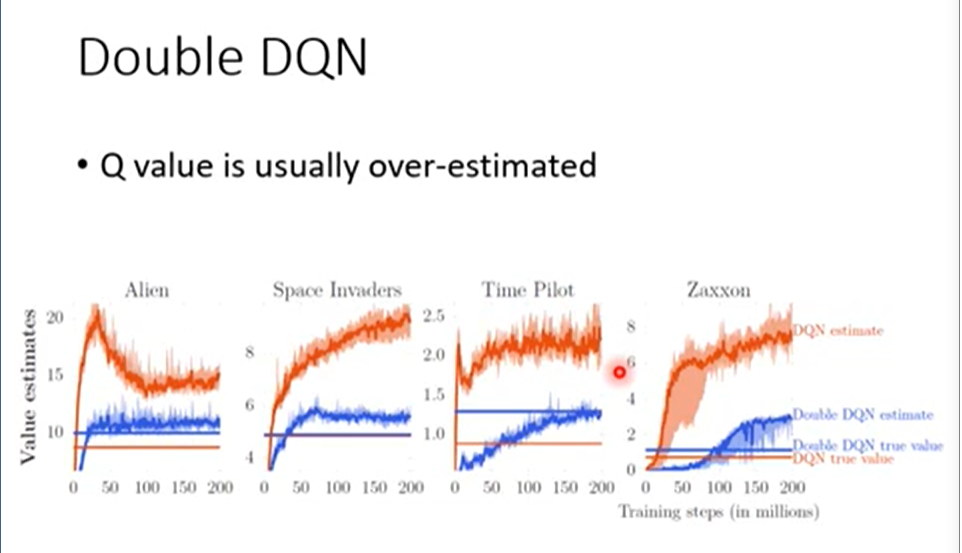
在神经网络估计Q的时候，是会估计大，也会估计小的。但是由于选择的是会带来最大Q的action。所以往往估值过高的那个action会被选择。 （从直观来理解，在选取最大值的机制下，被高估的值更容易被选中，进而也导致了高估。）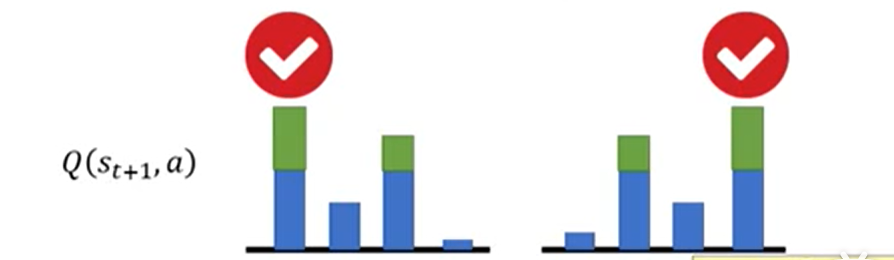

• 如何解决？使用double DQN：

即使Q网络高估了某个action，也没关系，因为Q value最终是由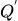算的。即使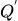会高估某个action也没关系，只要Q不选那个action就行了。从统计学的角度上来说更不容易产生过估计的”巧合”。

• 在实际应用中，由于本来就有两个Q的network，一个是target network，一个是Q network。用这两个network去算就可以了。

• Dueling DQN:

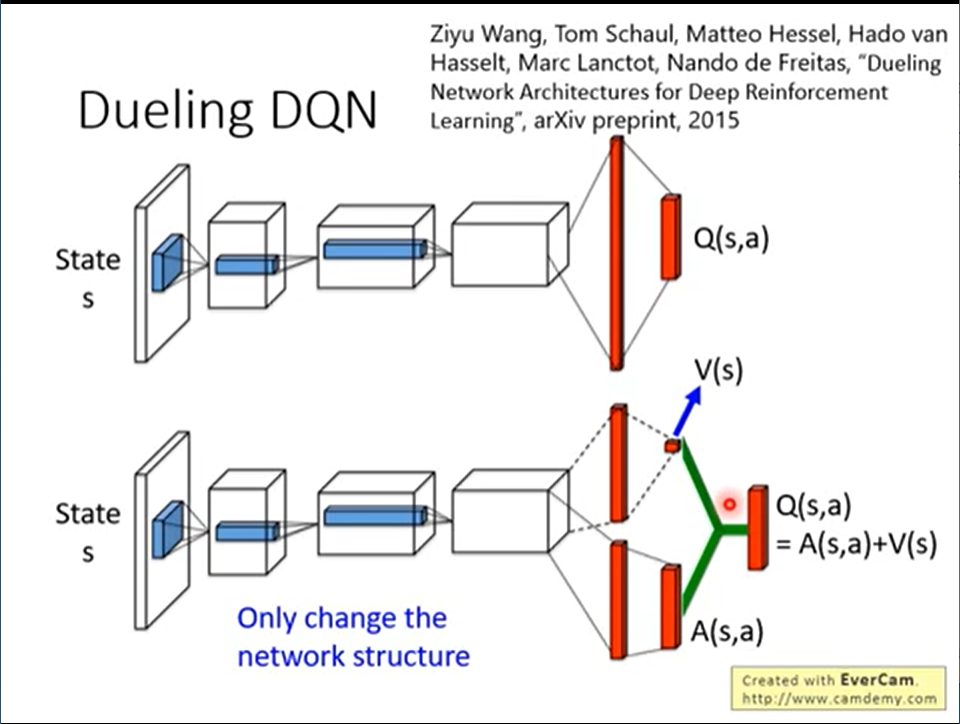
dueling DQN的本质其实就是改了网络的架构。之前的网络直接输出一个Q的vector。现在的网络是生成一个A vector和一个V vector。例如：

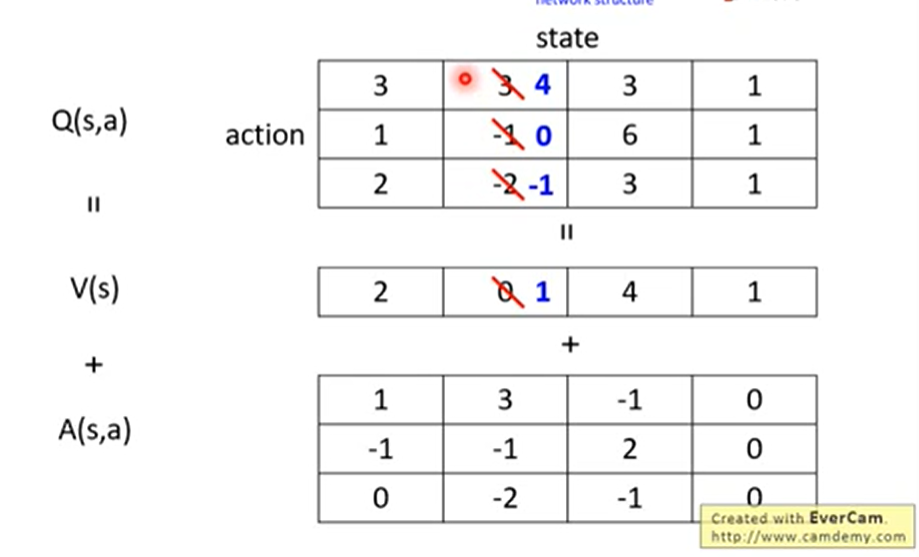
在某一个state，可能只sample到两个action。但是如果改了V，第三个action相对应的Q值也会发生改变。这样就会比较有效率。为了避免over trainning，会对A加一些约束。例如，每一列的和都为0。或者在生成A的network的最后一层中，对A做一个normalization：

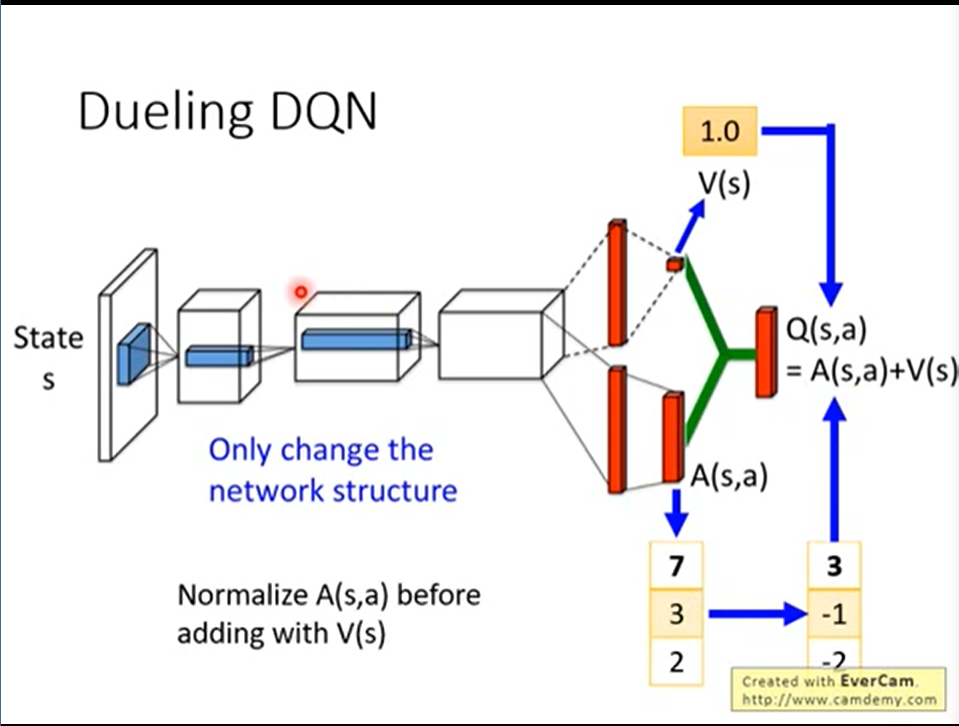
• Prioritized Reply：直觉的解释是从experience buffer中sample一些数据进行train的时候，sample每个pair的概率都是相同的、随机的。这样存在的问题是，如果某一个pair，网络总是学不好，那么应该增加这个pair被sample到的几率，让网络多学几次。Prioritized Reply就是解决这个问题（这里只做了解）。

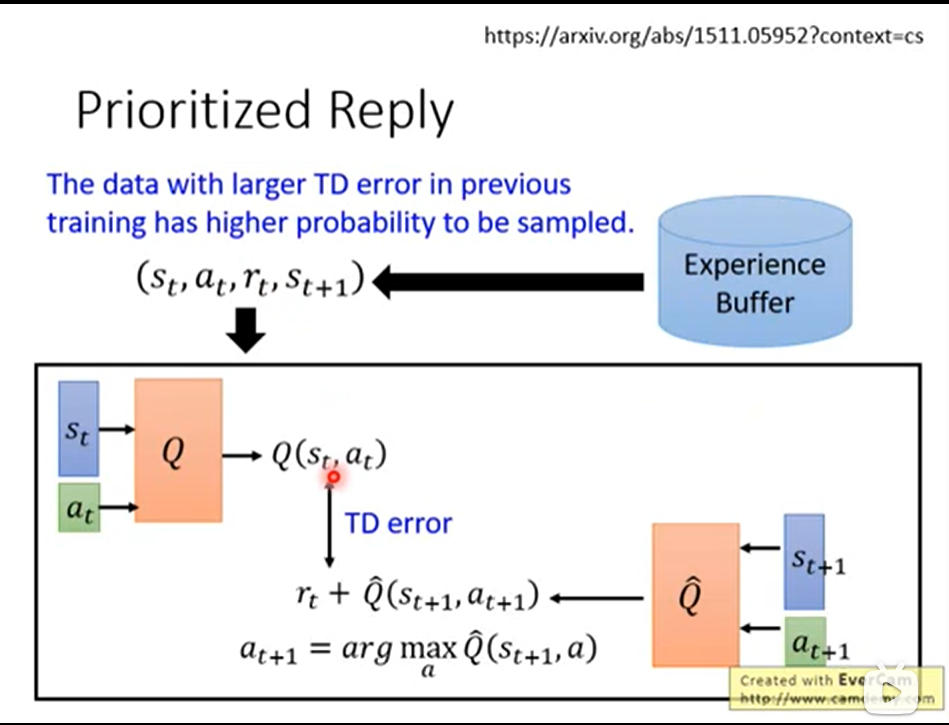
• Multi-step

使用TD的算法模式，但是不是比较每次step的Q network和target network的差异，而是比较几个时间步下，也就是observation history下的值差异。也就是融合了TD和MC。这里的N是一个需要调节的超参数。

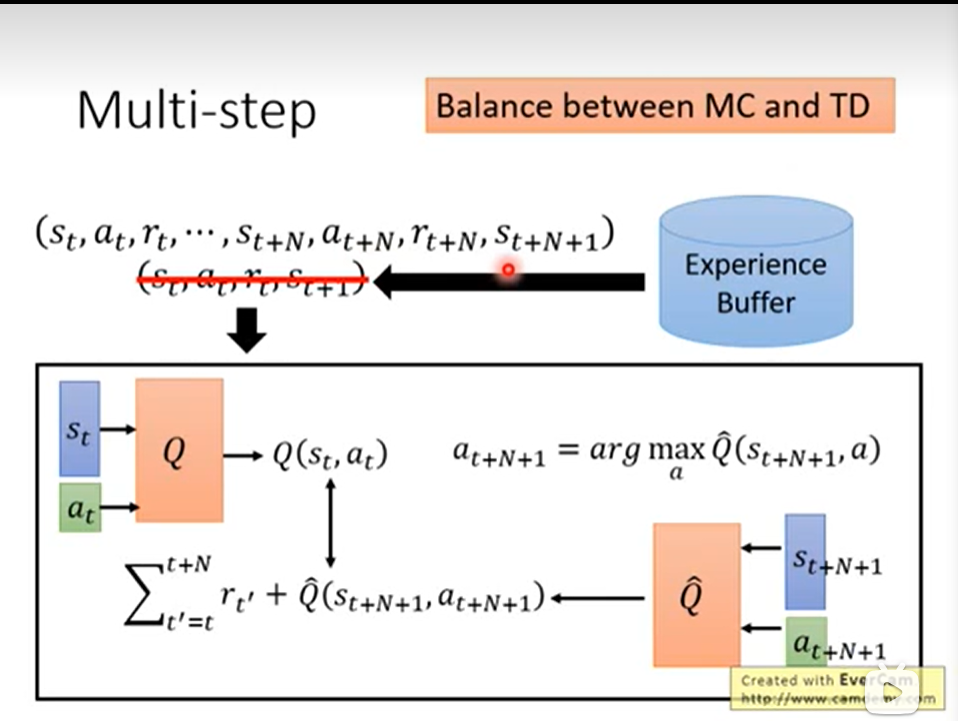
• Noisy Net

说白了就是对Q这个network的每一个参数，在每一个episode开始前，都加上一个噪声（例如高斯噪声）。

优势：贪心Epsilon Greedy在某一个state下，他的输出的action是可能不一样的。例如有可能是最优action，也有可能是random。但是在Q网络上加噪声，在一样或者相似的state下，agent输出的action是一样的。

• Distributional Q-function

传统的Q network是根据state输出采取不同action的Q值。而这个Q值其实是一个random variable。并不是说我们在这个state下采取这个action，就一定会得到一个固定值的Q。因为环境是有随机性的。因此Distributional Q-function是直接输出这个Q的分布。

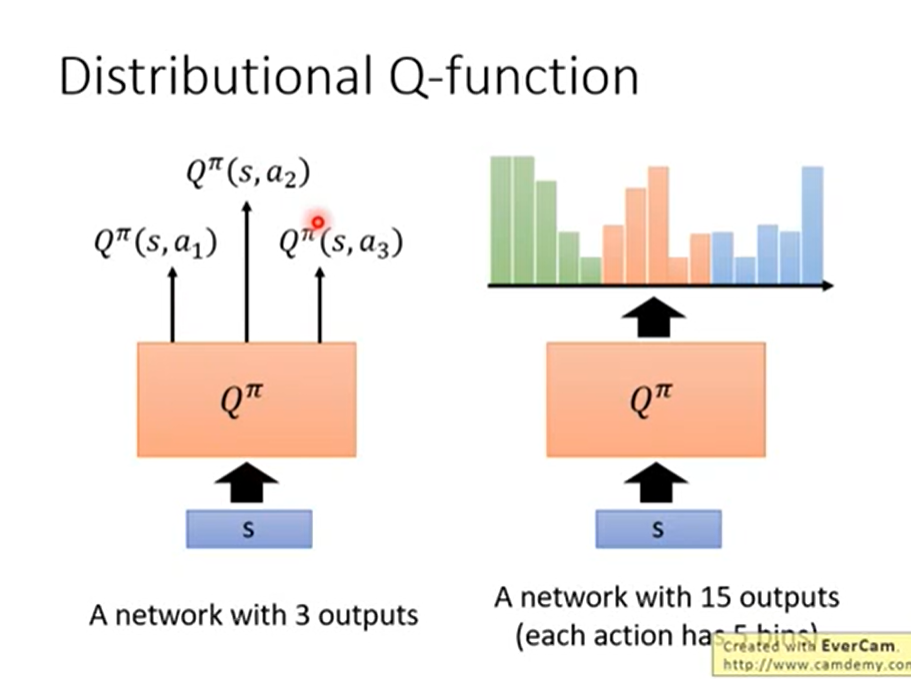
这个方法目前应用较少，但是一个可能的应用是假如两个action的Q的mean值类似，但是其中一个action对应的Q方差较大，这样就可以选择领一个，规避风险。

• rainbow

把所有方法合在一起。

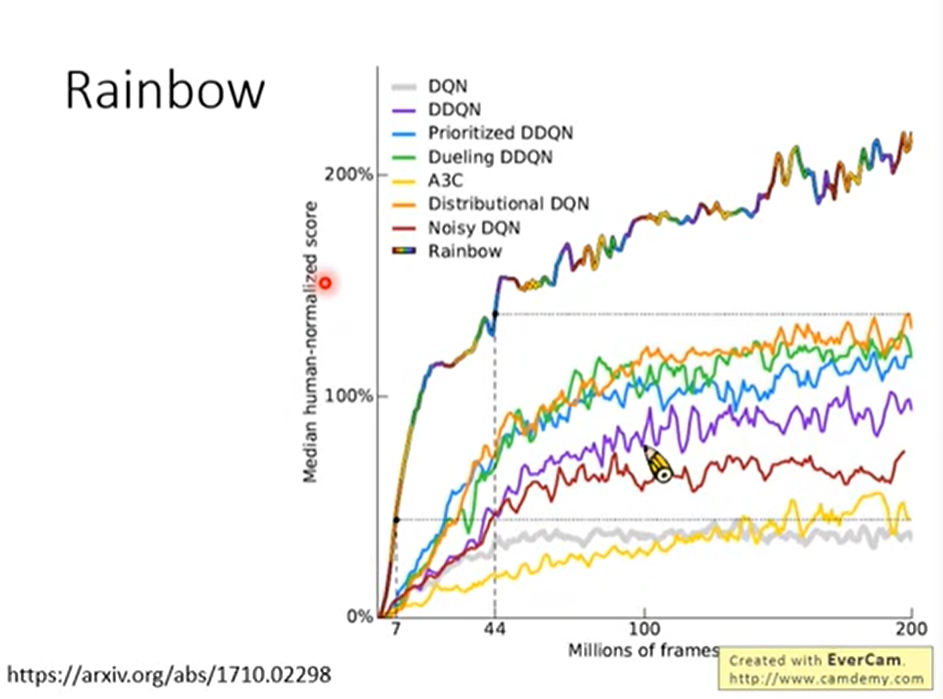
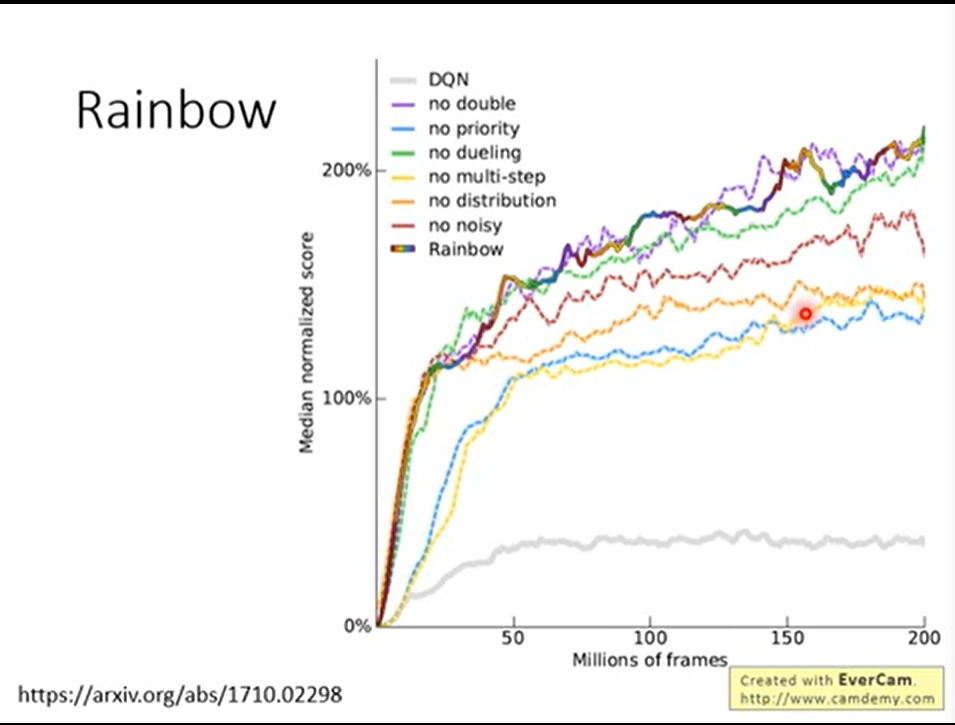
Q learning（Continuous Actions）

• 如果action不是离散的，而是连续的，那在计算Q value时，如何选择最好的action就不会很好选了。有三种解决办法：

1. sample一大堆action，然后选Q最大的那个action。

2. 使用gradient ascent。

3. 设计一个network，让最优化更简单。

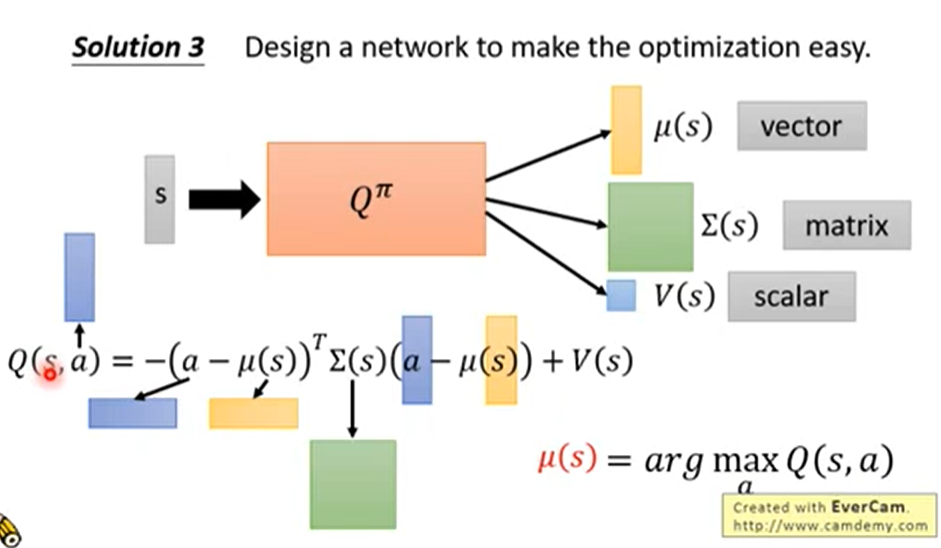
第三种方法是最好的。个人理解有点像SVD分解。由于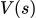前面的值总是负的，想要Q最大，则：

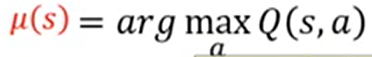
Actor-Critic

• 考虑到policy gradient的定义：

根据定义，括号里的前一项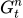表示在当前时刻t下执行action 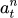时的累积奖励，也就是Q fuction的定义。后面的baseline b可以有多种取法。一个常见的取法是，使用V function。这里的意义是，我们在每个状态下都考虑了当前策略的预期回报，然后通过实际回报与预期回报的差值来调整策略，这样可以更加稳定的进行策略优化。

• 实际操作中根据Q function的定义，可以忽略期望值E，而是考虑当前的值就是Q值。这样就可以只考虑一个V，train一个network就好了。这样会导致方差变大。但是由于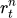本身只是一个step下的小reward，所以就还好。

• Actor-Critic的算法如下：

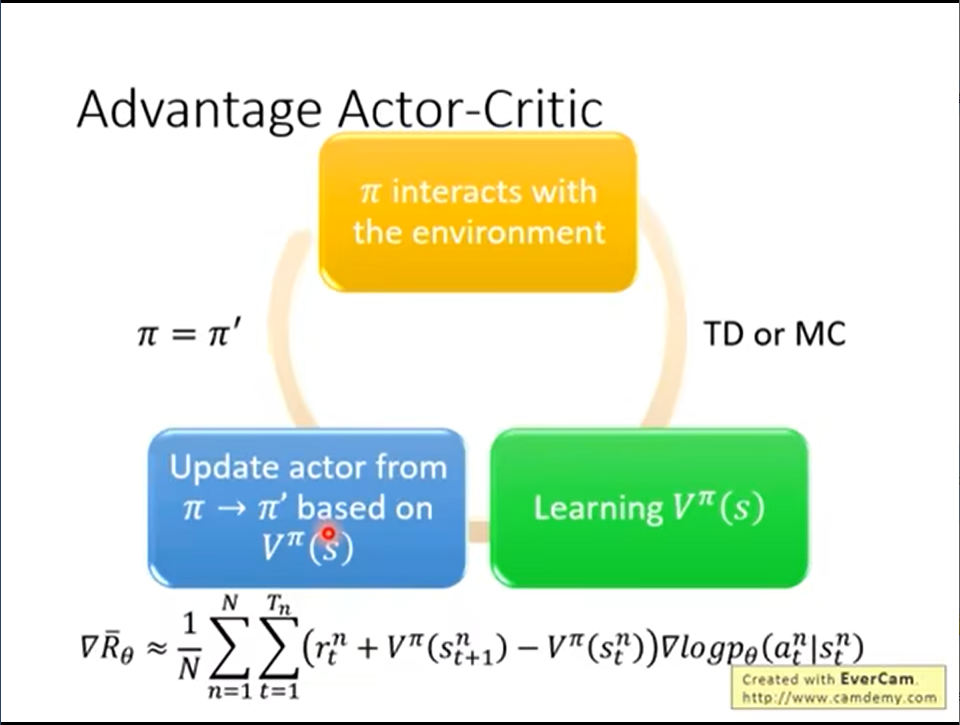
• Tips 1：actor和critic的一些参数（前几层）是可以共享的。

• Tips 2：对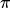网络下一个约束，即entropy要大，即不同的action被采用的几率平均一些。这样更有利于sample不同的action。

• A3C： 一开始有一个global的network。然后开很多的worker。每一个worker都先把blobal的network的参数copy过来，然后和环境互动，计算gradient，再传回global的network。

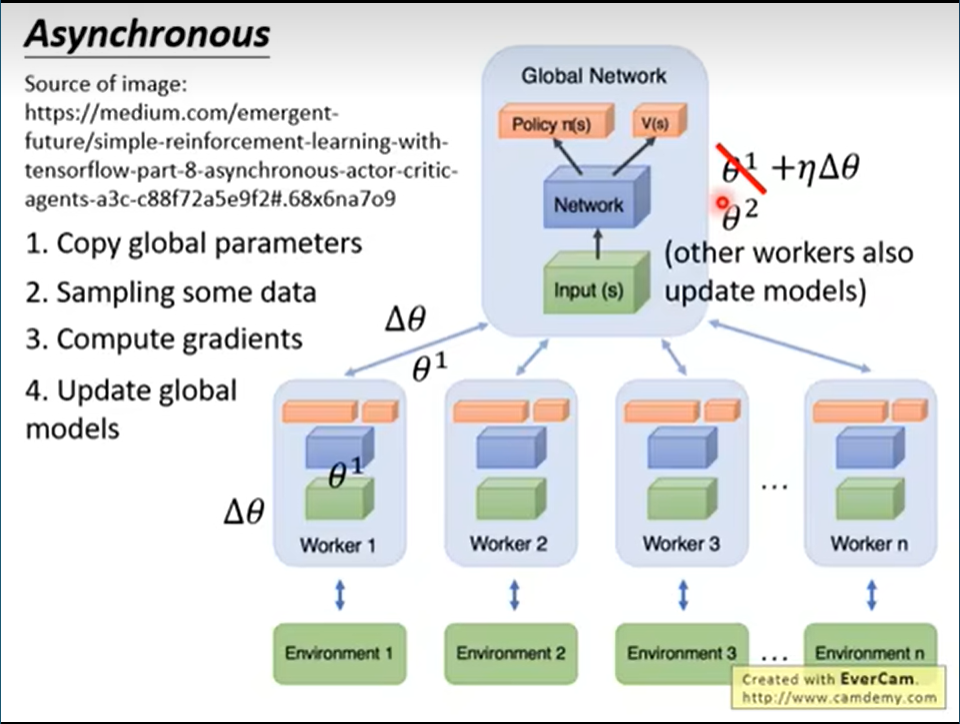
• Pathwise Derivative Policy Gradient

如何用Q learning解连续的action问题？考虑actor是一个解Q value最大的solver。

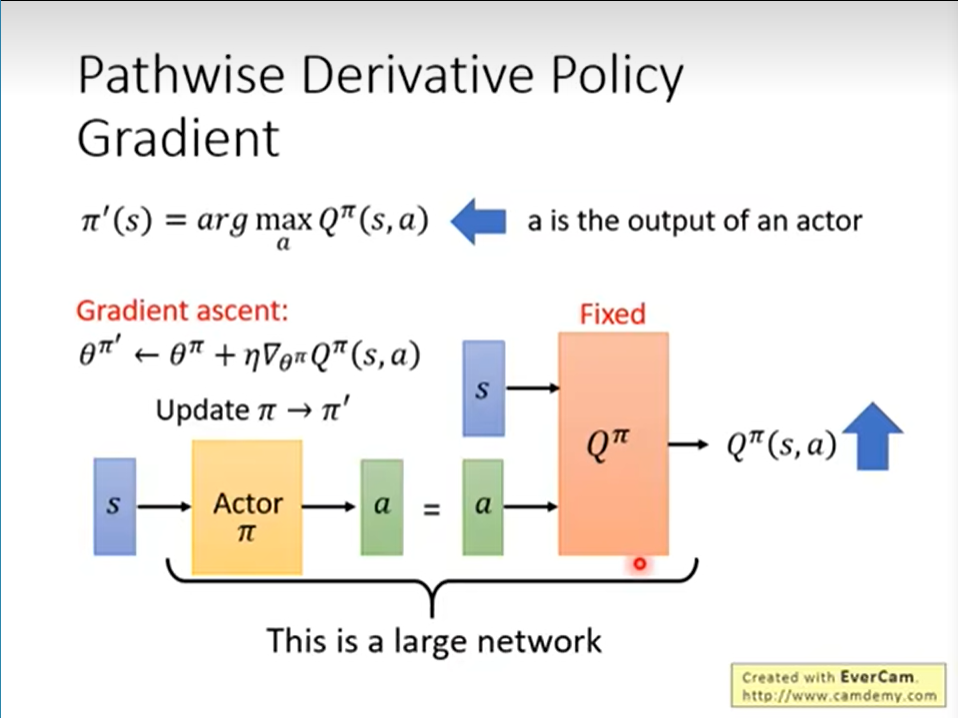
流程是，一开始有一个policy和环境做互动，然后用TD/MC的方法来估计Q值。之后把Q network参数固定，learn actor，目的是让他的a可以让Q的值越大越好。

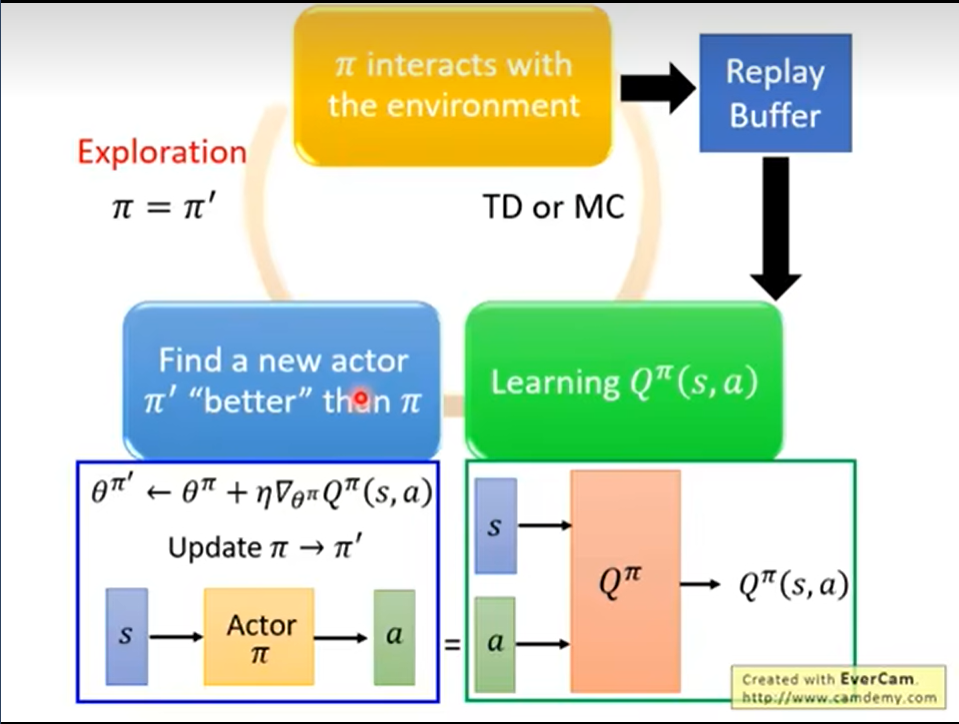
完整算法：

Sparse Reward

在强化学习的训练过程中，当环境的reward很少时（指出现的次数），这样对agent的训练是很不利的。比如，让一个机器人拿起螺丝刀，再把螺丝拧进去才能得到reward。这一系列操作组合起来对于一个一开始什么都不懂的机器人无疑是很难的，因为它一开始不管做什么动作都不会得到reward，即便有exploration也只有极小的几率能成功获得reward。

所以下面介绍几种方法来处理这种Sparse Reward的方法。

• Reward Shaping

既然环境的reward很稀疏，那我们就自己设定一些假的reward去引导agent往我们想要的方向。

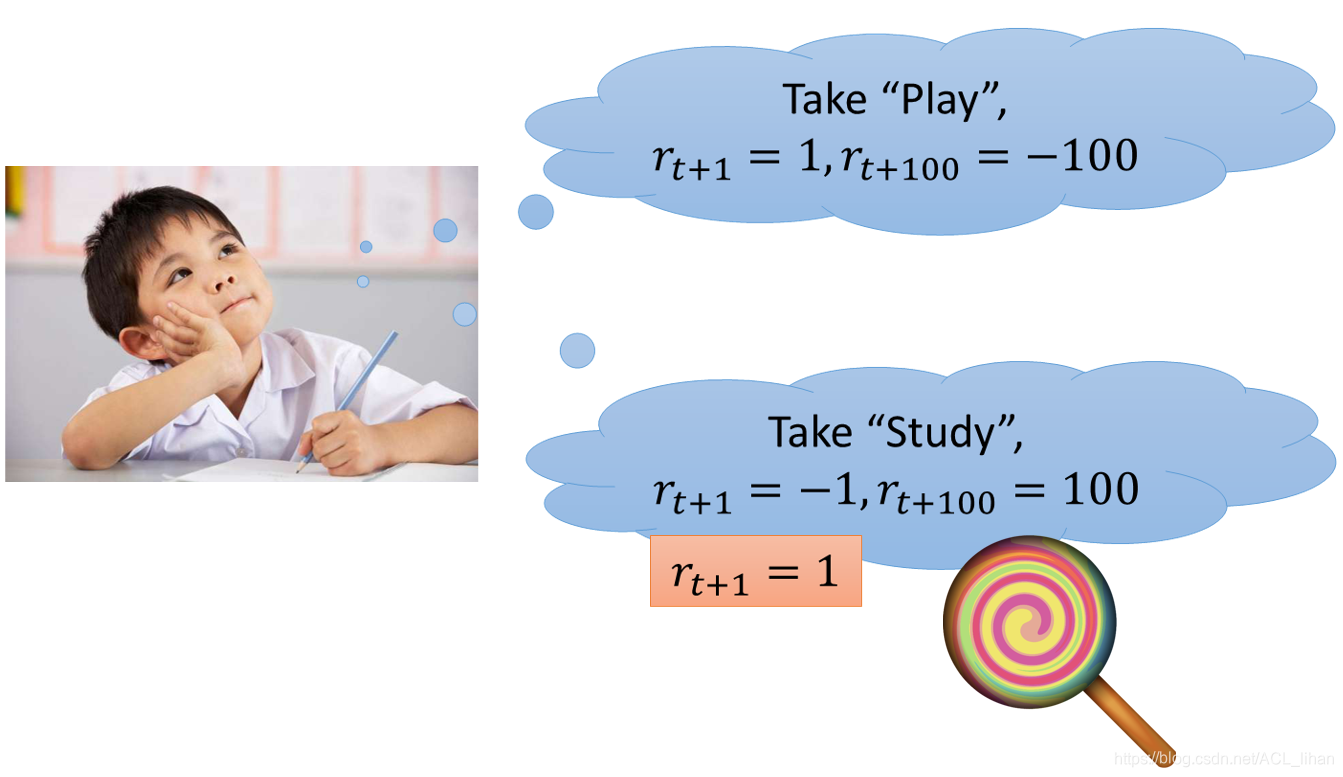
举个例子，这里agent是这个小孩。它有两个动作，如果选择出去玩，短时间内能得到reward +1，但是之后的考试可能很很差（reward -100）；如果选择学习，短时间内可能会不爽，所以reward是-1，但是之后能获得reward +100。

所以，为了引导这个小孩（agent）能往去好好学习，就会骗他说坐下来念书给棒棒糖吃，所以对他来说下一个时间点的reward就变成+1。然后他就会选择学习这个动作，即便这个reward不是实际存在的。

这是一个比较简单的例子，所以比较容易假设。而在现实中要引导agent需要设定正确的reward才能得到好的训练效果，这个reward可能不是很直观就能想到的。

所以下面要介绍一些比较通用的可以加进去reward。

• Curiosity

由于环境中的reward很少，导致agent不知道要干嘛，一直在里面瞎转。所以要制造一些reward使这个agent去探索一些没做过的事情，其实这是一种exploration的技术。

以论文（https://arxiv.org/pdf/1705.05363.pdf） 中的提到的例子，在Mario游戏中，智能体(Mario)纯粹利用好奇心进行探索，而不从杀死敌人或者躲避危险中得到任何激励信号。这样的智能体仍然学会了如何杀死敌人和躲避攻击。原因是因为被敌人杀掉会导致智能体只能看到一小部分的游戏空间，从而迅速导致其好奇心饱和。为了保持"好奇心"，智能体必须学会杀死敌人和躲避危险，以到达更多更新的游戏空间。（此段落参考博文:https://blog.csdn.net/triplemeng/article/details/84912694）

下面看具体的过程：

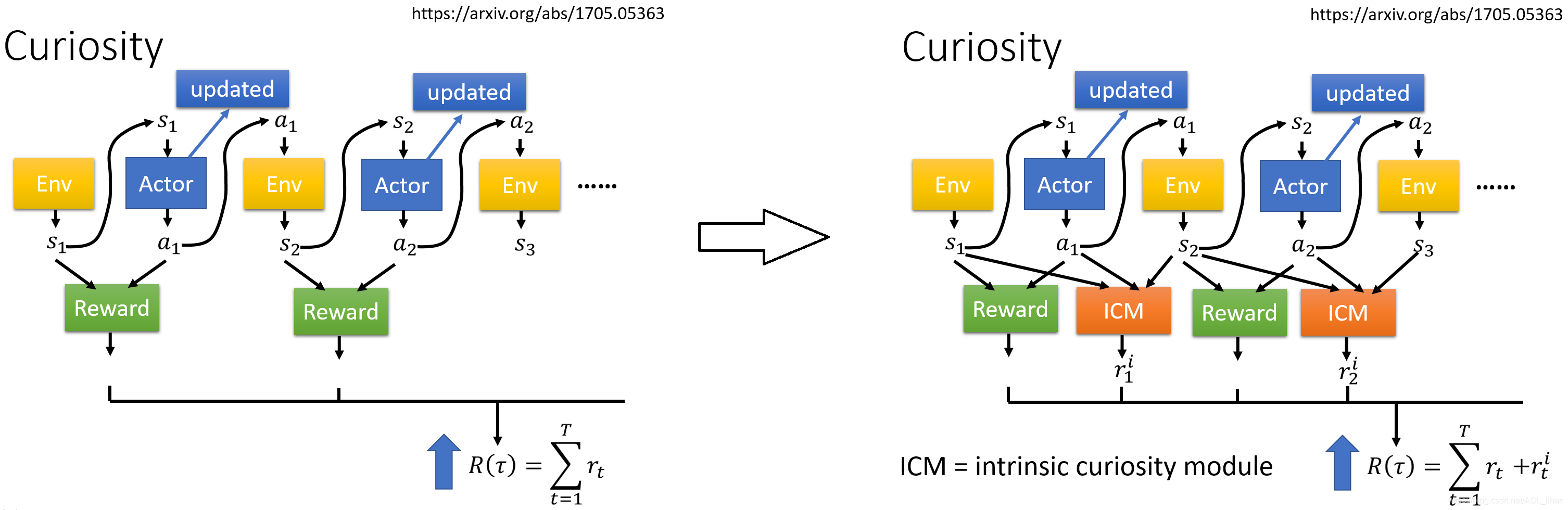
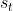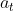左图是之前的图，以在执行获得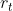。然后累加整个过程的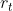作为total reward。

右图是加入Curiosity技术的ICM模块的图，ICM以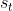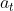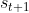，，为输入，输出一个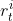，然后累加整个过程的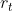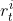，的总和作为total reward。所以现在不仅希望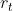越大越好，还希望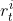也越大越好。

• ICM的设计

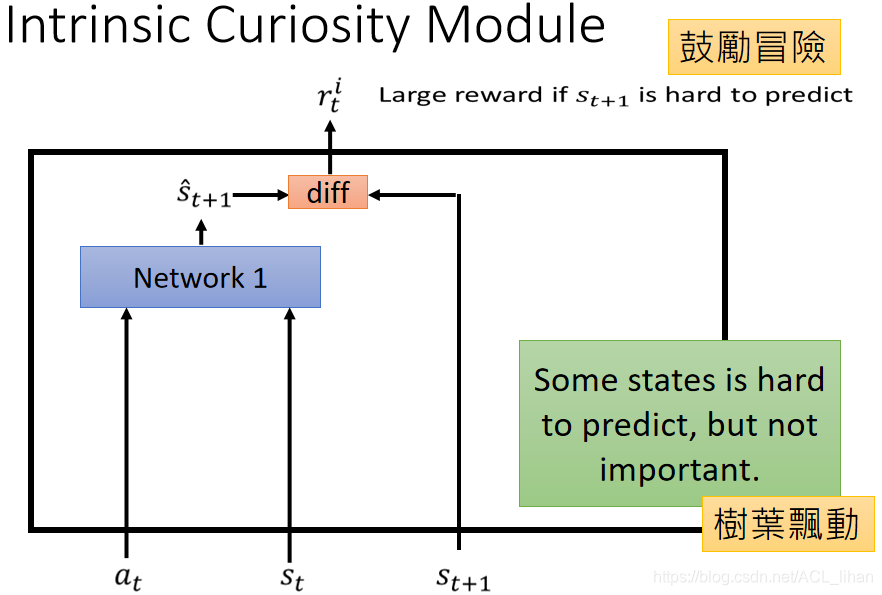
输入到ICM的，作为模块中的一个网络Network 1的输入，去预测接下来会遇到的状态，然后和实际下一个状态去作对比。预测的状态和实际的状态越不像，这个reward就越大，所以agent就会越倾向于去冒险以满足自己的好奇心。

注意：其中的Network 1是另外训练出来的，训练好后在ICM中运用的时候，它的参数是被固定住的。

这是ICM最原始的样子，但是这是不够的。因为在实际中，有一些state虽然难预测，但是不代表就要让agent往这些state靠近，有可能这些state是无关紧要的。比如agent站下树下看树叶飘动，而树叶飘动很难预测，但是由于好奇心驱使就导致agent一直站在原地看树叶飘动了。

所以需要让agent知道哪些事情才是应该要关注的。

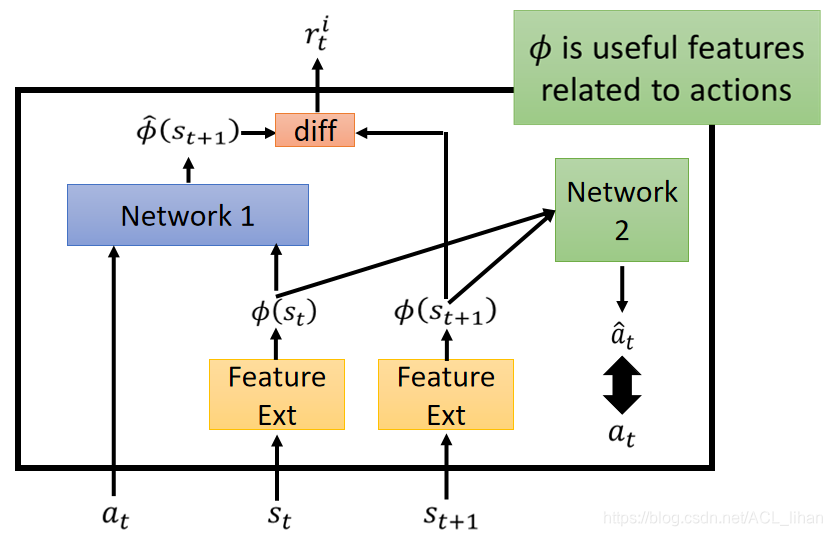
在刚才的基础上，再增加Feature Ext这个网络，Feature Ext先提取特征（这一步可以理解为把状态输入CNN后把游戏画面变成电脑看得懂的东西），再送到Network 2去预测由跳到需要执行的动作。把和实际做的动作作对比，如果比较接近则说明、是有用的状态；如果相差较大，则说明、是和agent要采取的动作无关的没用场景，这时就把这些状态过滤掉。

• Curriculum Learning

给agent安排学习计划，先从简单的题目开始学，学会以后再学习难的题目，就像我们从小学读到大学这样。

以Facebook的vizdoom为例子，他们让agent和不同等级的怪物打斗，先从速度慢血量薄的训练起，再慢慢和更强的怪物打斗。他们也有尝试过一开始直接让agent和最强的boss打，然后发现完全训练不了。

知道让agent从简单学起，但是还要知道如何给它设计课程，这时就可以用Reverse Curriculum Generation。

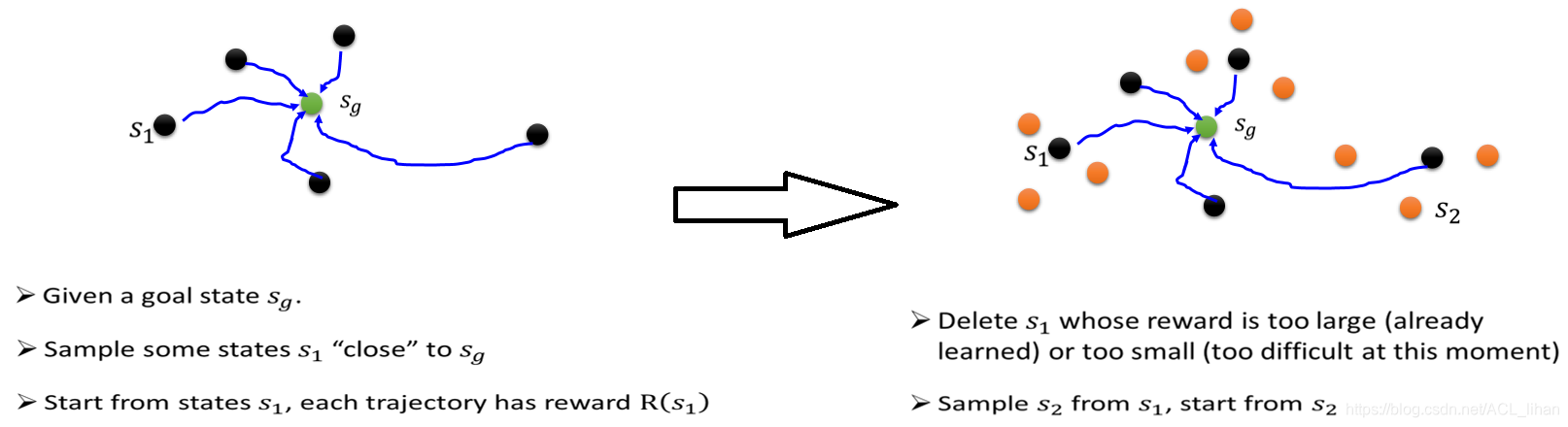
假设是目标状态（完成任务的状态），先从附近找出一些点，让agent从这些地方出发，往靠近。 到达后算出各点的reward，删掉reward最大（agent已经学会的，就没必要再学）的点和reward最小（目前还是萌新的agent觉得太难）的点，根据刚才删掉后剩下的点，继续寻找越远的点，再学习靠近。

• Hierarchical RL

把一个大的任务，通过上层agent的不断分解，让下层的agent去完成子任务。

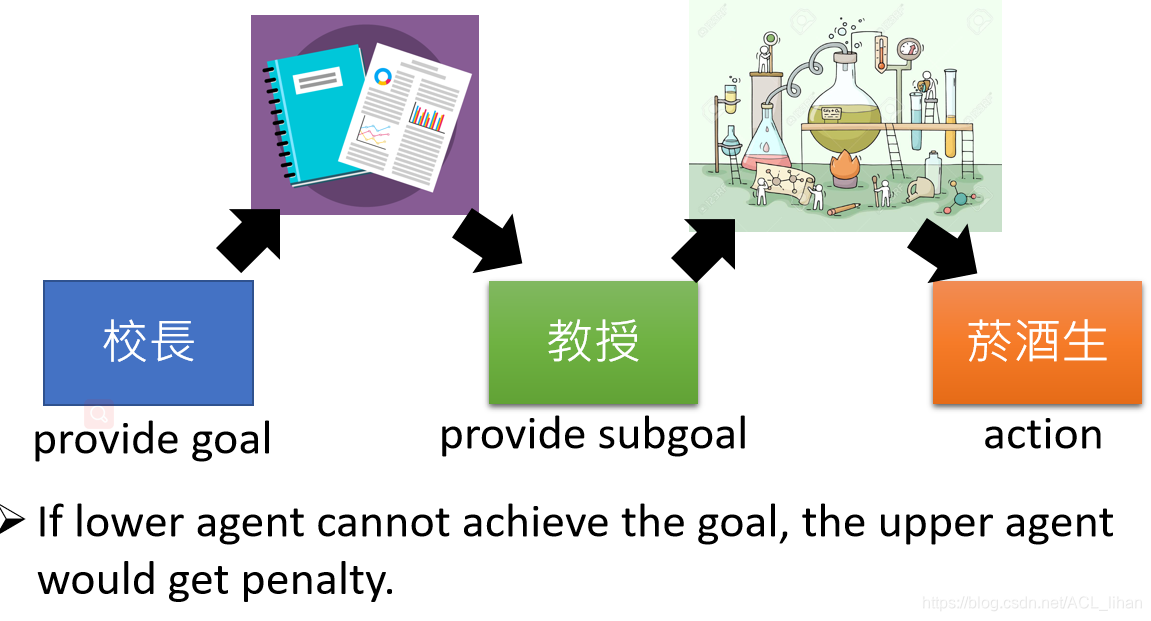
以上图为例子：校长为了学校的建设，让教授每年发3篇期刊；而教授把实验规划做好后，就让下面的研究生去干活。

其中注意一点，如果上层agent一直弄一些很难的任务给下层agent，导致下层agent没办法完成，上层的agent就会得到负的reward。

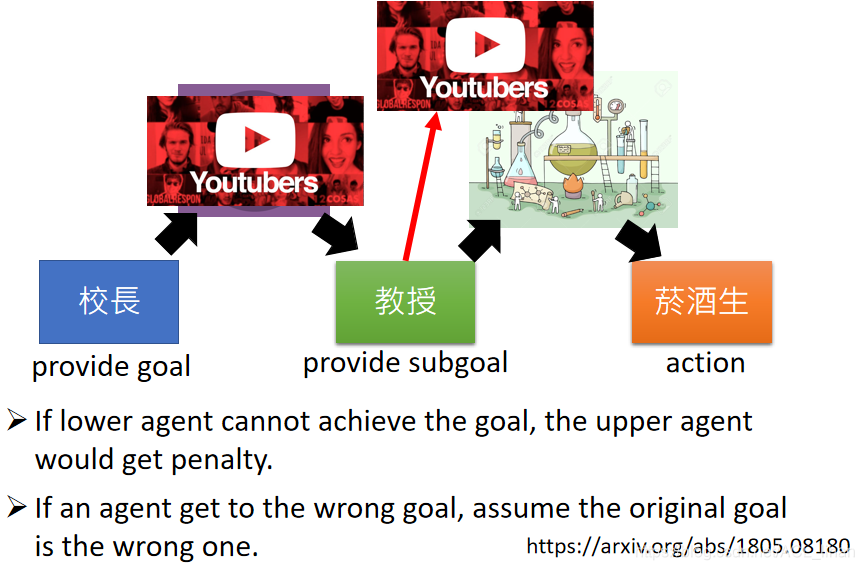
另一点要注意的是，如果下层的agent到达一个错误的目标，那为了下层做过的action不被浪费掉，就把上层原来目标改为这个错误的目标。以上图为例子，原本校长要求教授发期刊，但是教授后来经过探索却变成YouTubers，那校长就只能把原来的目标改成要求教授成为YouTubers。

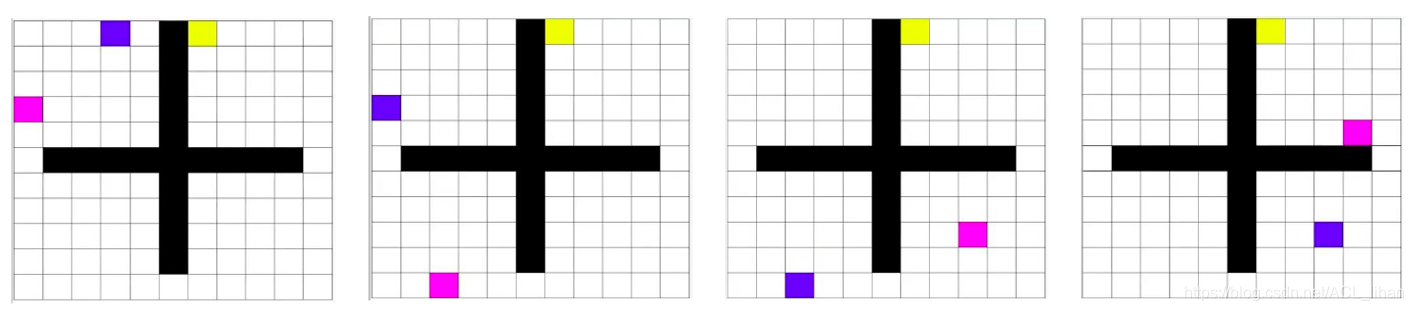
再举例子就是这个，紫色点代表下层的agent，粉色点代表上层agent的愿景，黄色点代表目的地。

这个任务中，把紫色点到目的地（黄色点）的路线，拆成4个子任务，让下层的agent（紫色点）跟着上层agent的愿景（粉色点）走，最终到达目的地（黄色点）。

Imitation Learning

上文讲了reward很稀疏的情况，但是在实际中，可能问题还会更进一步：很多场景是很难有一个明确的reward甚至没有reward。所以需要很厉害的agent或者直接由人来示范的资料，让agent跟着做。

• Behavior Cloning

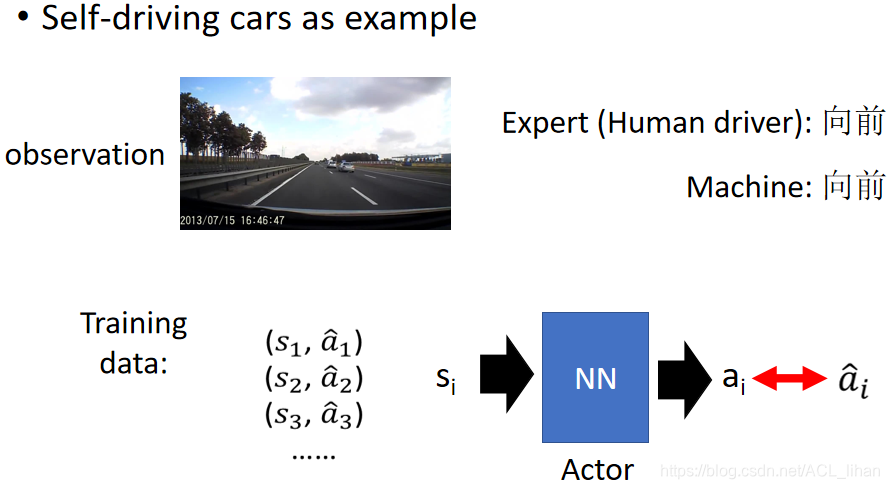
Behavior Cloning其实和监督学习（supervised learning）是一样的。 以自动驾驶为例子，搜集很多的expert（假设是人类）驾驶资料，这些资料的状态s是开车的场景，动作a是在此场景下做出的动作。把这些资料输入到Neural Network中，使网络输出的动作能尽可能接近实际人类做出的动作，就完成任务。

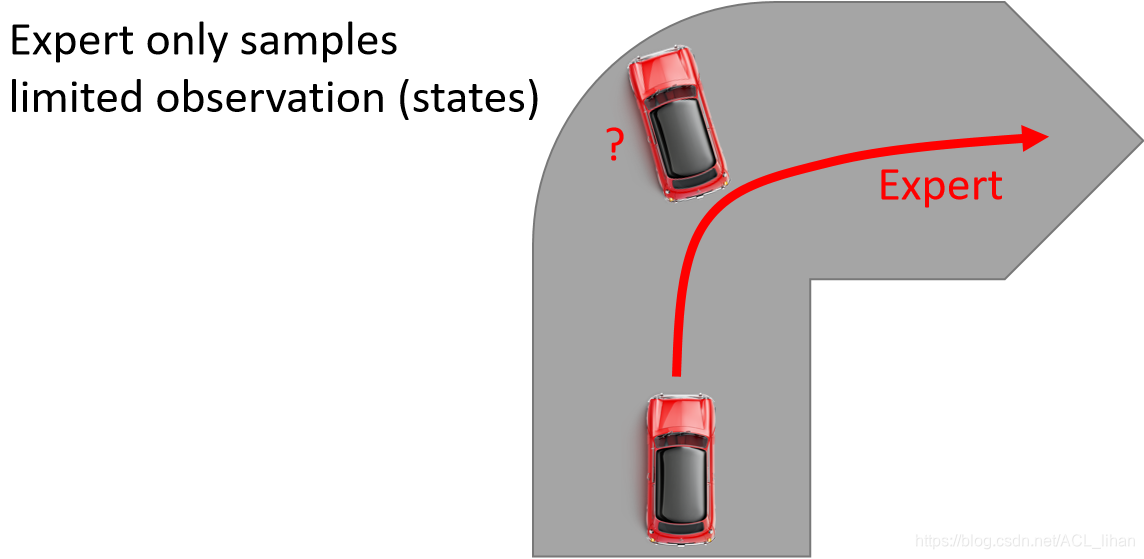
但是这个过程中，expert观察到state是有限的。比如在实验中，让人去开车，都能顺利转弯，没有出现撞墙的情况。而这时让agent去开车，如果某一时间它没及时转弯导致处于快撞墙的state，由于缺少相应的训练资料导致agent不知道接下来怎么做。

所以这时需要引入Dataset Aggregation稍微缓解下这个问题。

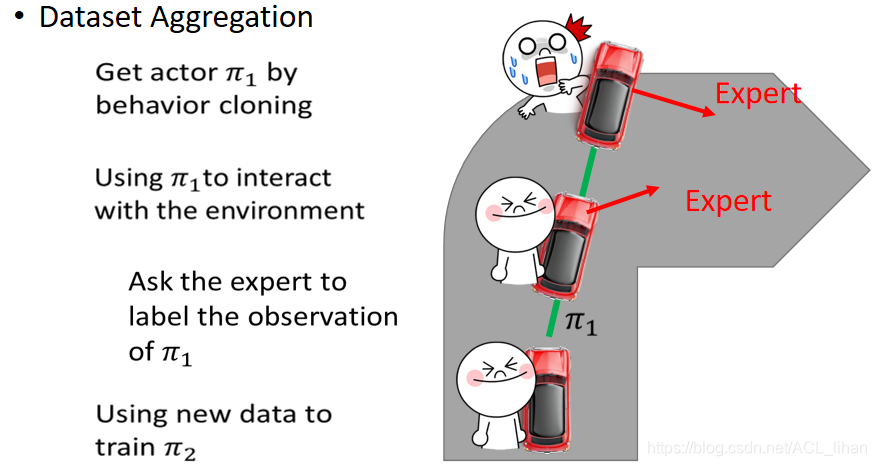
• Dataset Aggregation

1. 让actor 开车

2. 让一个专家坐在车子里观察所处状态并告诉actor 做出什么动作。

3. 但是actor不会听取专家的建议，还是以actor的意愿去开车，最终就撞墙了，一个episode结束。

4. 这时actor就知道在快要撞墙的时候要采取什么样的动作，然后用这个新的data去训练新的actor 。

5. 重复1234步……

从上面我们可以看出Behavior Cloning很容易实现，但是它也有问题：

1. agent会完全复制expert的行为，不管这个行为对不对

2. agent的学习能力有限，没办法什么都学，有可能只学到不好的东西，没学到有价值的东西

3. 有可能会遇到Mismatch的问题（上面开车那个例子）

在监督学习中，是希望训练数据和测试数据有独立同分布的。而在Behavior Cloning中，actor做出的action是会影响后续的state的。因为Network的训练是有误差的，训练出来的actor 不可能完全和expert actor 一模一样，就会导致某个state下，两者采取的action不一样，然后就导致后面的state完全不一样了，最坏的情况就是actor后面遇到的state是expert没遇到过的，这时actor就会完全不知道如何进行下去了。即，失之毫米，差之千里。

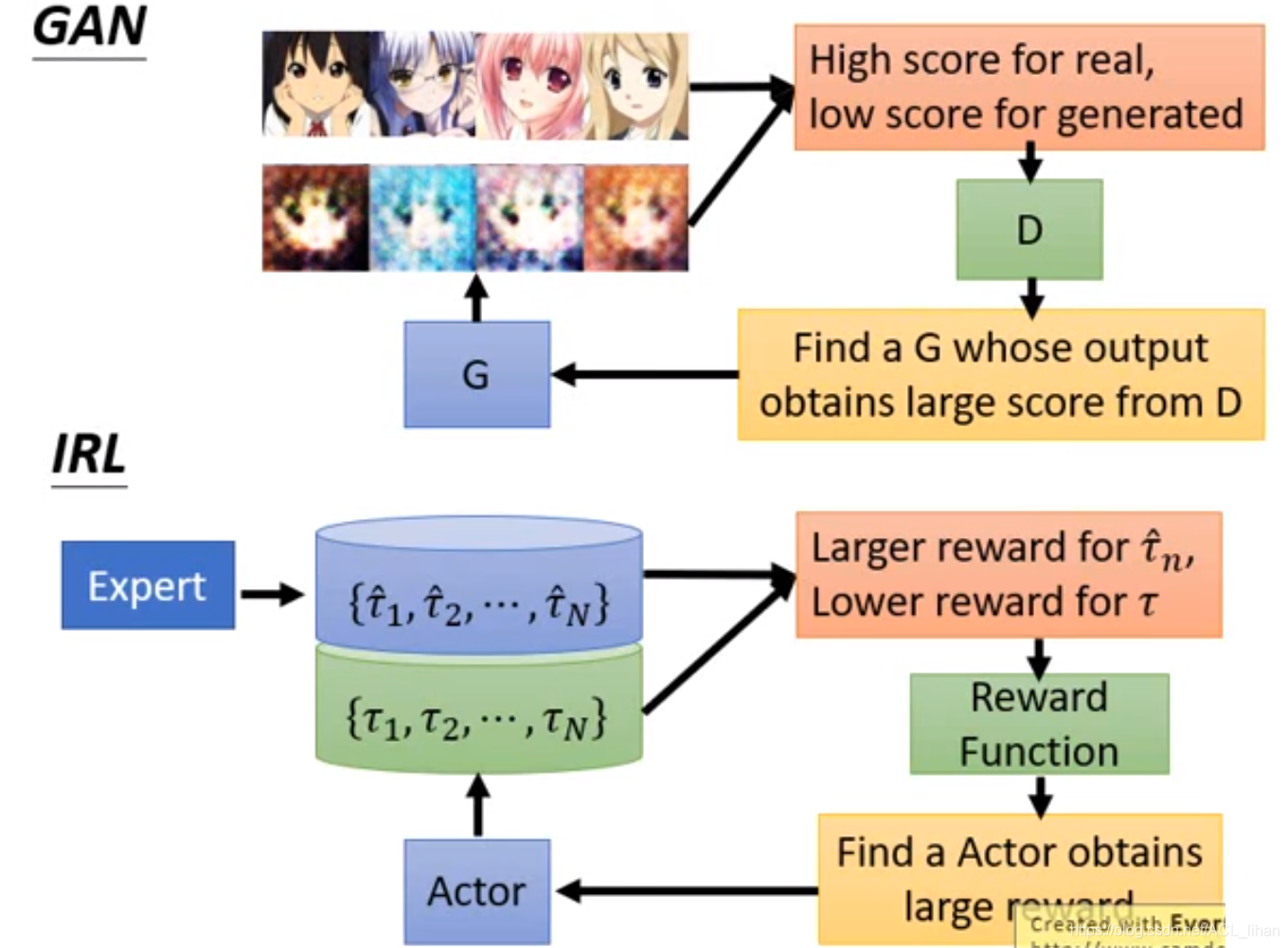
所以，虽然Behavior Cloning简单但是并不是一个很好的办法，所以又有第二种方法Inverse Reinforcement Learning (IRL)

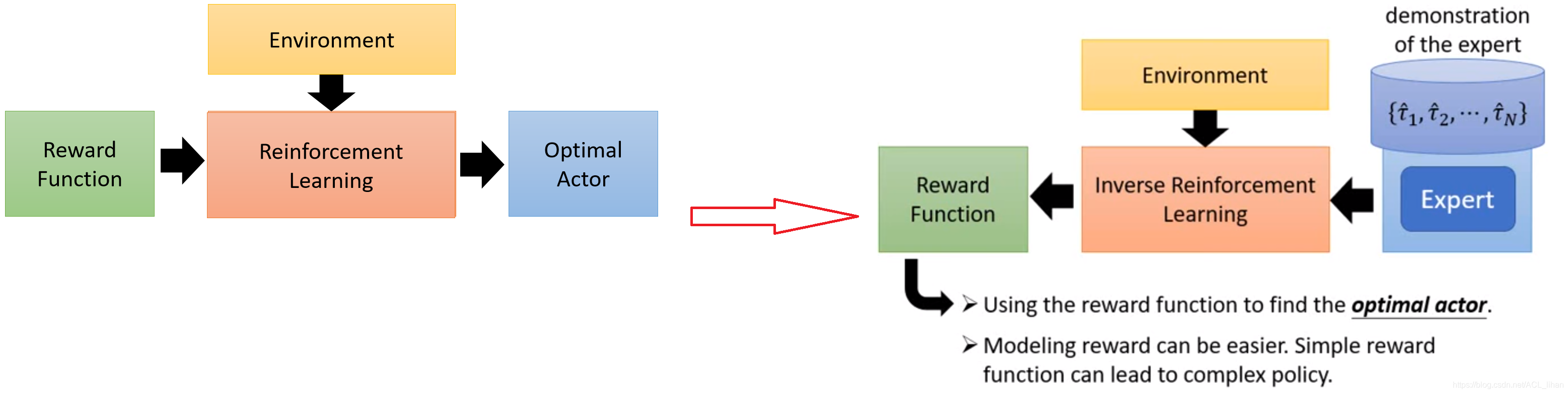
左图是熟悉的Reinforcement Learning的步骤，通过Environment和Reward function，最终更新出理想的Actor。

右图就是 Inverse Reinforcement Learning 的步骤，由于没办法从Environment获得reward，那就通过收集expert的资料还有Environment的信息，来反推Reward function，推出Reward function就能应用以前的Reinforcement Learning的做法了。

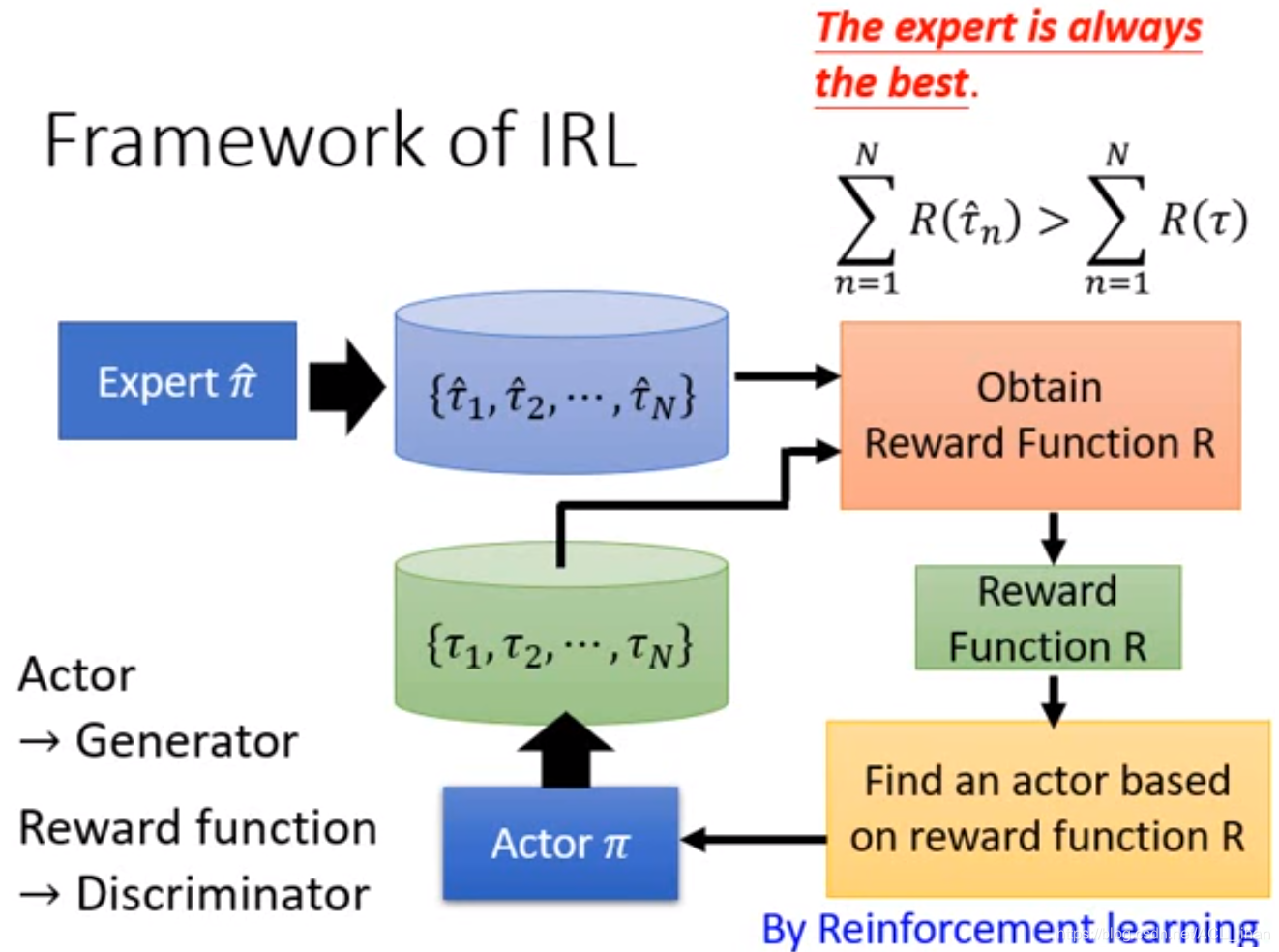
具体来看Inverse Reinforcement Learning怎么运作的。

1. expert 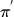去玩游戏，记录游戏过程，形成n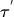个，每个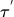代表1个episode。

2. actor 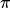去玩游戏，记录游戏过程，形成n个。

3. 设定一个Reward Function，这个Reward Function强制要求expert的累计得分一定要高于actor的累计得分。

4. 有了Reward Function就可以使actor去更新出更强的actor。

5. 当actor能在此时的Reward Function达到很高的reward时，修改Reward Function（还是要求expert的得分一定要高于actor），让actor根据新Reward Function去更新出更强的actor。

6. 重复上述步骤。

Inverse Reinforcement Learning可以实现只用很少量的expert的示范资料，就训练出一个很理想的actor。

看了以上的步骤，可以想到，actor和reward function就对应类似于GAN的generator和discriminator。通过reward function的不断修改，使actor越来越接近expert的水平。