关于搜索算法的复习

1. 为什么需要查找算法？

Rational Agent需要执行一系列行动，以实现目标。这种情况下可以给Agent提供一个“行动手册”，告诉它什么情况下该做什么事。

但是“行动手册”很难构造，因为很难直接预料到事情可能发生的所有情况。

所以更一般的方法是Agent了解世界以及其行为如何影响世界，通常通过搜索由世界状态构成的的内部建模空间来完成。

2. “解决问题”的任务

给定：

• 世界的初始状态。
• 可执行的一组操作。
• 目标检测：该检测可以被应用到世界的每一个初始状态上，来判断这个状态是不是目标状态。

寻找：

• 以状态和运算符路径形式的解决方案，显示如何将初始状态转换为满足目标测试的状态。
• 初始状态和运算符集隐含的定义了一个状态空间，即执行一个操作序列后，都可以从初始状态到达的一个目标状态。

3. 表现的衡量

• 路径成本Path Cost：一个为路径分配成本的函数，通常通过将路径中各个运算符的成本相加。总是希望找到成本最低的解决方案（最优）。
• 搜索成本Search Cost：找到解决方案所需的计算时间和空间（内存）。
• 通常的解决方案是在搜索成本和路径成本之间折中，目的是必须在可用时间内找到最佳解决方案。

4. 搜索策略

• 实施各种搜索策略的最简单方法是维护一个未扩展的搜索节点队列。
• 不同的策略源于在队列中插入新节点的不同方法。

搜索策略的属性：

• 完整性-保证找到解决方案（如果有）？
• 最优性-是否找到最佳解决方案？
• 时间复杂性-找到解决方案需要多长时间？
• 空间复杂度-搜索过程中需要多少内存？

5. 搜索算法

无信息的搜索算法	有信息的搜索算法
深度优先	贪婪最佳优先
广度优先	A*
一致代价	记忆有界的启发式
深度有限
迭代加深
双向搜索

无信息的都是暴力搜索。

6. Big O表示时间空间复杂度

教程：时间复杂度和空间复杂度，大O表示法【数据结构和算法入门2】

7. 无信息的搜索算法

无信息的都是暴力搜索。

7.1 宽度优先搜索

逐级展开搜索节点，在展开d+1级节点之前，将展开d级的所有节点。

•完备性-该算法最终访问给定深度的每个节点，当分支因子有限时他是完备的。
•最优性-提供的路径成本是节点深度的一个非减损函数时（例如，所有操作都有相同的成本），他是最优的（即节点到节点的费用与节点深度成正比）。

那么什么情况下不是最优的呢？个人理解：

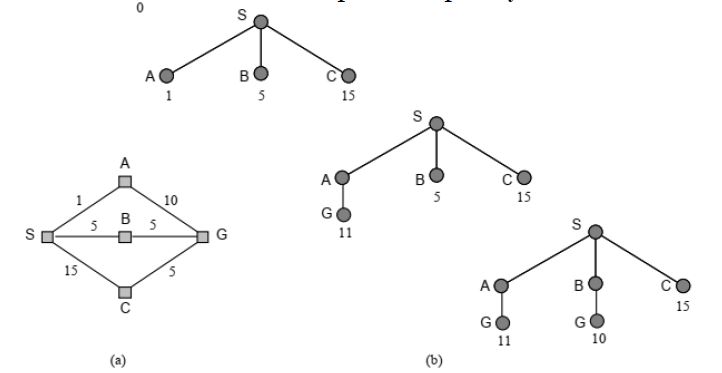
例如现在有ABC三个地点，以及他们的对应代价（比如A-C中间有个收费站，需要花5块钱）。

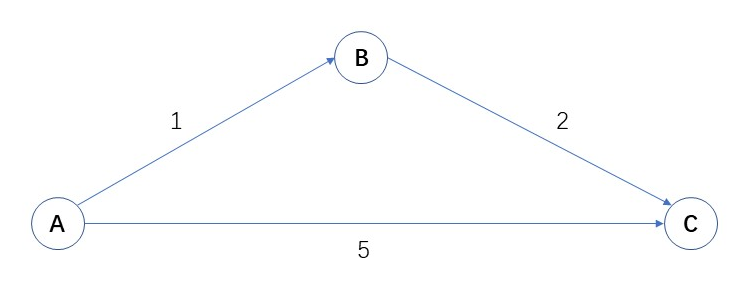
应用广度优先搜索求应该如何A到C。

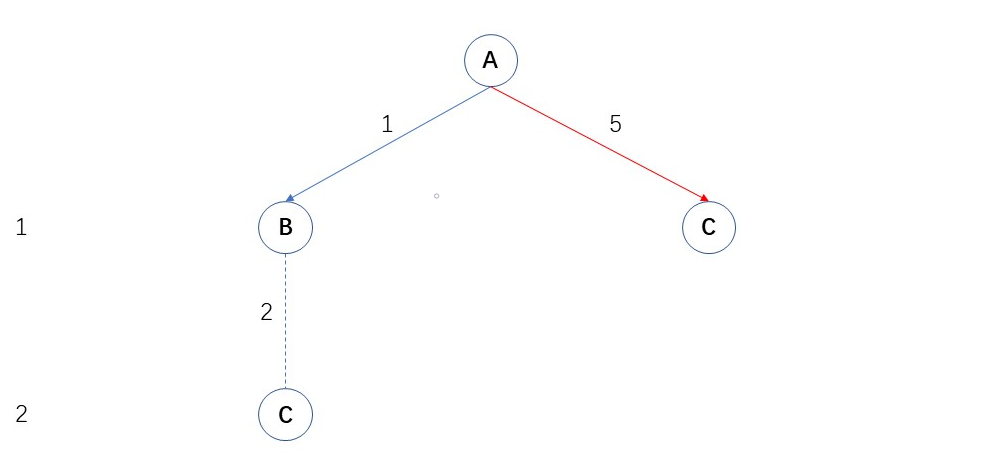
在第一级节点扩张的时候，他就找到了C，然后就中止（如果允许提前退出的话）。所以如果考虑路径成本的的话，直接从A到C并不是最优解。
但是这么做扩张的节点层数少，相应的节省了一点搜索成本。

7.1.1 宽度优先搜索的复杂度

假设每次平均扩展$b$个节点，称之为分支因子。

时间复杂度：找到深度$d$范围内的最佳解决方案，需要$1+b+b^2+...+b^d=O(b^d)$，即最坏需要遍历所有的点。

空间复杂度：需要内存大小为$O(b^d)$的边缘节点集。

7.2 一致代价搜索

与广度优先类似，不同之处在于总是扩展路径成本最低而不是深度最小的节点（即按路径成本对新队列排序）。

直到目标是队列中成本最低的节点（即，当进行扩展时当发现目标节点），才识别目标。

因此，具有非负数的阶跃成本最优（在最坏情况下也意味着更高的时间和空间复杂度）

7.3 深度优先搜索

始终在树的最深处展开节点，即最近生成的节点之一。当遇到死胡同时，回到最后的选择。（不撞南墙不回头，一路走到黑）

7.3.1 深度优先搜索的属性

• 不完备的：可能会沿着无限路径迷路。
• 非最优解：可以在探索较浅的解决方案之前找到更深的解决方案。
• 时间复杂度：最坏情况下为$O(b^m)$，注意$m$（状态空间的最大深度，可以为无限大）可能比$d$（目标结点的深度）大。
• 空间复杂度：$O(bm)$，$m$为树的最大深度。队列只包含从根节点到叶节点的一条路径，以及路径上每个节点的其余同级节点。
• 可以添加深度限制𝑙 防止探测超过给定深度的节点。

咋理解这个空间复杂度呢? 深度优先算法的优势在于，在开辟一个新节点的时候，只要保存一条路径上的同级节点即可。

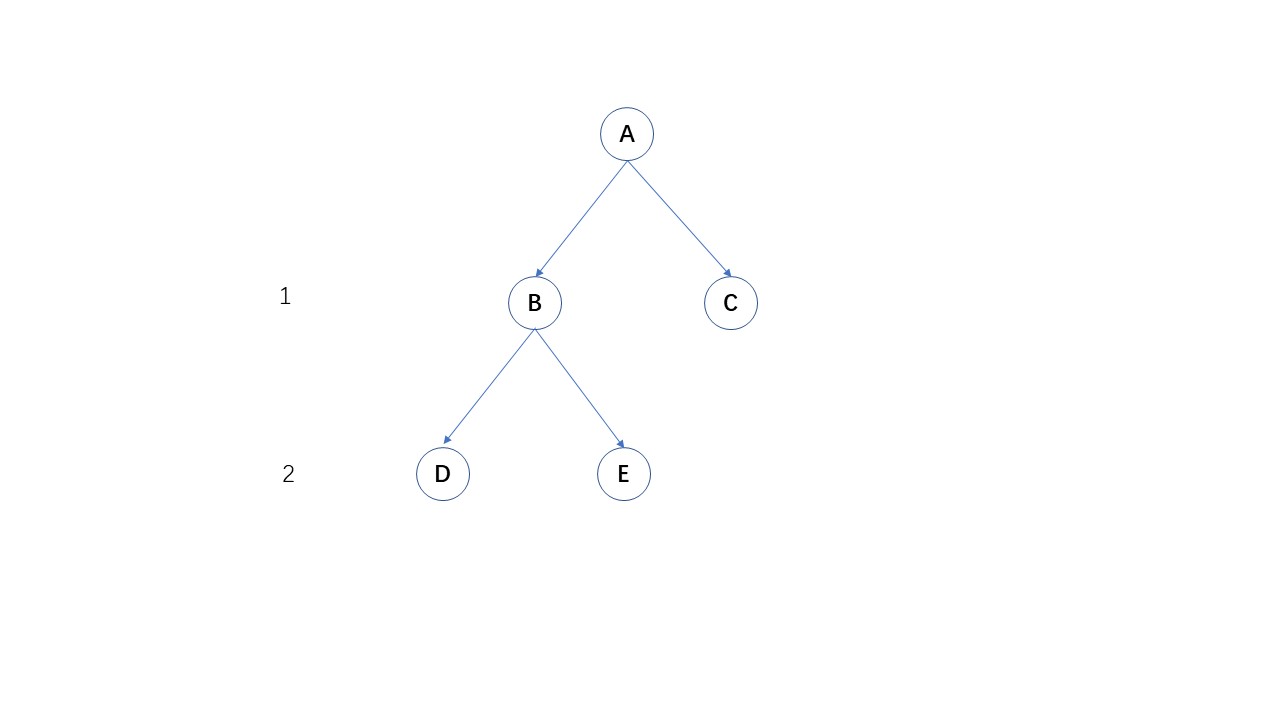
在这种情况下，空间复杂度为$O(2\times2)$

7.4 迭代加深的深度优先搜索

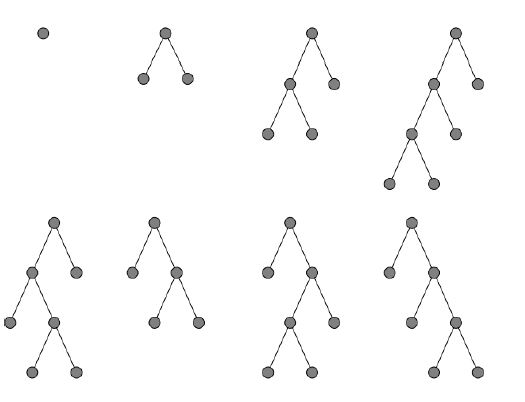
做法是不断增加深度限制来应用深度优先搜索，0，1，2……d，直到找到目标。

这种情况并没有增加多大的$cost$，因为大多数节点都在下方，上方多生成几次无所谓的。

底层节点生成了一次，倒数第二层节点生成了两次，以此类推，所以一共生成了$(d)b+(d-1)b^2...+(1)b^d$个节点。

• 时间复杂度：$O(b^d)$
• 空间复杂度：$O(bd)$

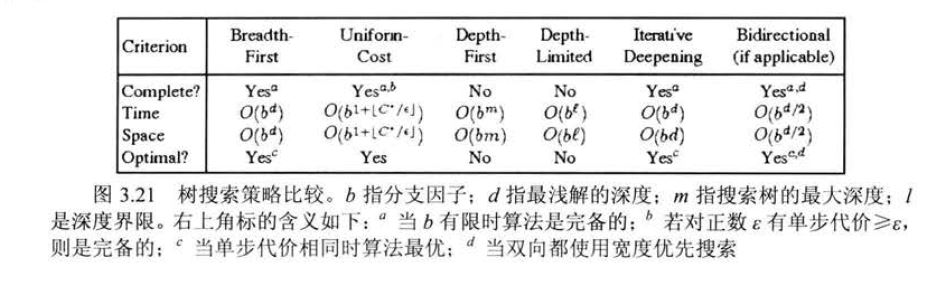
7.5 无信息搜索策略总结

8. 减少重复

减少重复检测同一状态的方法：

1. 不跟随自循环（将分支移动回相同的状态）。
2. 不创建具有循环的路径（删除路径上已存在的返回根的分支）。
3. 不要生成任何已生成的状态。需要存储所有生成的状态并搜索它们（通常使用哈希表以提高效率）。

9.有信息的搜索算法

非暴力。

9.1 贪婪最佳优先搜索

我想去北边的德克士，但是我不知道路。那我一直往北走摸过去就好了。

$f(n) = h(n)$;

• 不完备的：可能会沿着无限路径迷路。（如果启发式h合理的话这种情况可以避免）
• 最优性：不是最优的。
• 时间复杂度：最坏情况下为$O(b^m)$，注意$m$（状态空间的最大深度，可以为无限大）可能比$d$（目标结点的深度）大。
• 空间复杂度：最坏情况下$O(b^m)$。

但是，高质量的启发式可以大大减少时间复杂度和空间复杂度。

9.2 A*

$f(n) = g(n)+h(n)$; $g(n)$是$cost$函数。

• 时间复杂度：最坏情况下为$O(b^d)$
• 空间复杂度：最坏情况下$O(b^d)$

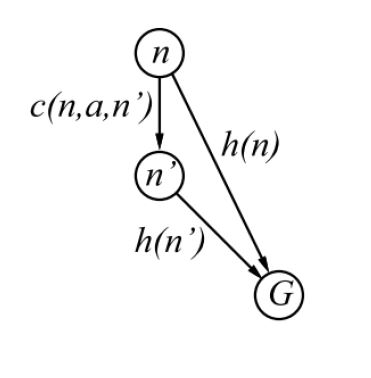
对于树搜索： 最优性的保证是$admissible$的启发式，即启发式h(n)要小于等于$h(n')$。其中$h(n')$为真实的损耗。
对于图搜索： 最优性的保证是$consistent$的启发式, $h(n)\leqslant c(n,a,n')+h(n')$

$consistent$的理解：如果对于每个结点$n$和通过任一行动$a$生成的$n$的每个后继结点n’，从结点n到达目标的估计代价不大于从$n$到$n'$的单步代价与从$n'$到达目标的估计代价之和.

说人话就是两边之和不能大于第三边，即通过启发式估计出来的损耗路径要比真实的小。

9.2.1 A*的速度和准确率

1. 如果启发式$h$等于0，那么就只考虑代价搜索，成一致代价搜索了。是可以找到最优解的，但是搜索成本大。
2. 如果启发式$h(n)$准确的等于$h(n')$，那搜索成本特别小，找到的也是最优解。但是这种情况太理想了（特殊情况下才可能实现）！
3. 如果启发式$h(n)$过大，那他就不考虑前面的cost了，相当于贪婪最佳优先搜索了。

结语

我说怎么看了Ola的ppt一天也没看明白，原来ppt上是错的……

学好数据结构很重要。

参考

[1]StuartJ.Russell, PeterNorvig, 诺维格,等. 人工智能:一种现代的方法[J]. 清华大学出版社, 2013.

一个好玩的算法可视化网站: 红色斑点