前言
本来是想学学数据结构的,看了黑马的教程,前面排序算法还好,后面几乎每一集的算法代码都有错误,业务能力捉急。就只记录排序算法的部分。
b站Java 数据结构 排序算法学习笔记整理。黑马程序员Java数据结构与算法,全网资料最全,154张数据结构图
1. 什么是数据结构
定义:
数据结构是一门研究非数值计算的程序设计问题中的操作对象,以及它们之间的关系和操作等相关问题的学科。
2. 数据结构的分类
分为物理结构和逻辑结构两大类:
逻辑结构:
- 集合结构:几何结构中数据元素除了属于同一个集合外,没有其他的联系。
- 线性结构:线性结构中的数据元素之间一对一的关系。
- 树形结构:线性结构中的数据元素之间存在一对多的层次关系。
- 图形结构:图形结构的数据元素是多对多的关系。
物理结构:
又称为存储结构。
- 顺序存储结构:把数据元素放到地址连续的存储单元里面,其数据间的逻辑关系和物理关系是一致的。(比如数组)
- 链式存储结构:把数据元素存放在任意的存储单元里,这组存储单元可以是连续的,也可以是不连续的。在链式存储结构中引用了一个指针存放数据元素的地址,这样通过地址就可以找到关联的数据元素的位置。(比如链表)
3. 大O表示法
规则:
- 用常数1取代运行时间中的所有加法常数。
- 再修改后的运行次数中,只保留高阶项。
- 如果最高阶项存在,且常数因子不为1,则去除与这个项相乘的常熟。
常见大O阶及其关系:
O(1)<O(logn)<O(n)<O(nlogn)<O(n2)<O(n3)
4. 冒泡排序
4.1 排序原理:
- 比较相邻的元素。如果前一个元素比后一个元素大,就交换这两个元素的位置。
- 对每一对相邻元素做同样的工作,从开始第一对元素到结尾的最后一对元素。最终最后位置的元素就是最大值。

在代码实现时,使用Integer来进行包装,因为Integer实现了 Comparable<Integer>这个类。
4.2 实现代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| package 冒泡排序;
public class bubble {
public static void sort(Integer[] numbers) {
for (int i = 0; i < numbers.length - 1; i++) {
for(int j = 0; j < numbers.length - i - 1; j++){
if(greater(numbers[j],numbers[j+1])){
exchange(numbers,j,j+1);
}
}
}
}
private static boolean greater(Integer num1, Integer num2) {
return num1.compareTo(num2) > 0;
}
private static void exchange(Integer[] numbers, int i, int j) {
Integer tempValue = numbers[i];
numbers[i] = numbers[j];
numbers[j] = tempValue;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
| package 冒泡排序;
import java.util.Arrays;
public class test {
public static void main(String[] args) {
Integer[] numbers = {1, 2, 3, 4234, 534, 7457, 6456, 432, -1, 0};
bubble.sort(numbers);
System.out.println(Arrays.toString(numbers));
}
}
|
4.3 时间复杂度
时间复杂度为O(N2)。
5. 选择排序
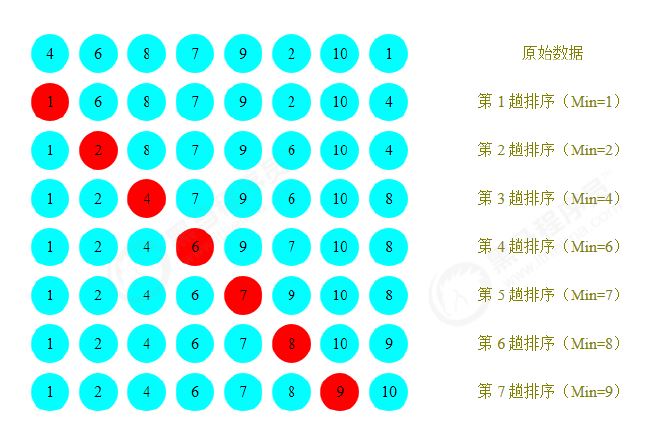
5.1 排序原理
- 每一次遍历的过程中,都假定第一个索引处的元素是最小值,和其他索引处的值依次进行比较,如果当前索引处的值大于其他某个索引处的值,则假定其他某个索引出的值为最小值,最后可以找到最小值所在的索引。
- 交换第一个索引处和最小值所在的索引处的值
5.2 代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| package 选择排序;
public class Select {
public static void sort(Integer[] numbers){
for(int i = 0; i < numbers.length - 1; i++){
int index = i;
for(int j = i + 1; j < numbers.length; j++){
if(greater(numbers[index],numbers[j])){
index = j;
}
}
exchange(numbers,i,index);
}
}
private static boolean greater(Integer num1, Integer num2) {
return num1.compareTo(num2) > 0;
}
private static void exchange(Integer[] numbers, int i, int j) {
Integer tempValue = numbers[i];
numbers[i] = numbers[j];
numbers[j] = tempValue;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
| package 选择排序;
import java.util.Arrays;
public class test {
public static void main(String[] args) {
Integer[] numbers = {1, 2, 3, 432, 534, 7457, 6456, 432, -1, 0};
Select.sort(numbers);
System.out.println(Arrays.toString(numbers));
}
}
|
5.3 时间复杂度
时间复杂度为O(N2)。
6. 插入排序
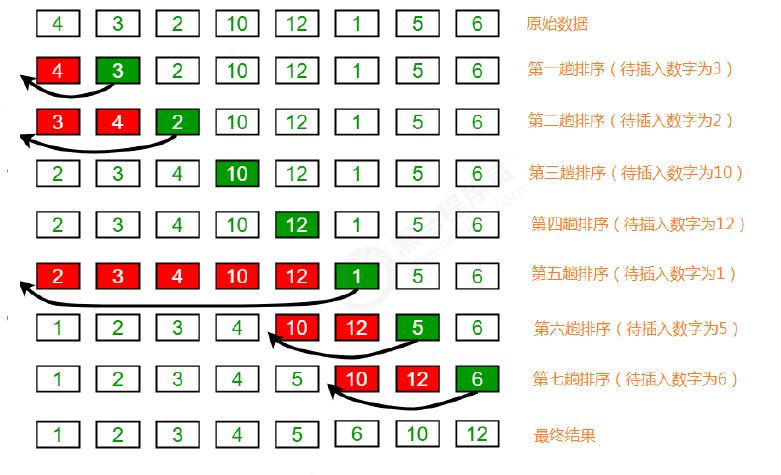
6.1 排序原理:
- 把所有的元素分为两组,已经排序的和未排序的;
- 找到未排序的组中的第一个元素,向已经排序的组中进行插入;
- 倒叙遍历已经排序的元素,依次和待插入的元素进行比较,直到找到一个元素小于等于待插入元素,那么就把待插入元素放到这个位置,其他的元素向后移动一位;
6.2 代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| package 插入排序;
public class Insertion {
public static void sort(Integer[] numbers) {
for (int i = 1; i <= numbers.length - 1; i++) {
for (int j = i; j > 0; j--) {
if (greater(numbers[j], numbers[j - 1])) {
break;
} else {
exchange(numbers, j, j - 1);
}
}
}
}
private static boolean greater(Integer num1, Integer num2) {
return num1.compareTo(num2) > 0;
}
private static void exchange(Integer[] numbers, int i, int j) {
Integer tempValue = numbers[i];
numbers[i] = numbers[j];
numbers[j] = tempValue;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
| package 插入排序;
import java.util.Arrays;
public class test {
public static void main(String[] args) {
Integer[] numbers = {7,6,5,4,3,2,1};
Insertion.sort(numbers);
System.out.println(Arrays.toString(numbers));
}
}
|
6.3 时间复杂度
时间复杂度为O(N2)。
7. 希尔排序
7.1 原理
- 选定一个增长量h,按照增长量h作为数据分组的依据,对数据进行分组;
- 对分好组的每一组数据完成插入排序;
- 减小增长量,最小减为1,重复第二步操作。
- 插入排序的一种改进。
- 增长量h的确定:增长量h的值每一固定的规则,我们这里采用以下规则:
1
2
3
4
5
6
7
8
| int h = 1;
while(h < 数组长度/2){
h = 2h+1;
}
h = h/2;
|

7.2 代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| package 希尔排序;
public class Shell {
public static void sort(Integer[] numbers) {
int h = 1;
while (h < numbers.length / 2) {
h = 2 * h + 1;
}
while (h >= 1) {
for (int i = h; i < numbers.length; i++) {
for (int j = i; j >= h; j -= h) {
if(greater(numbers[j-h],numbers[j])){
exchange(numbers,j,j-h);
}else{
break;
}
}
}
h/=2;
}
}
private static boolean greater(Integer num1, Integer num2) {
return num1.compareTo(num2) > 0;
}
private static void exchange(Integer[] numbers, int i, int j) {
Integer tempValue = numbers[i];
numbers[i] = numbers[j];
numbers[j] = tempValue;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
| package 希尔排序;
import java.util.Arrays;
public class test {
public static void main(String[] args) {
Integer[] numbers = {7,6,5,4,3,2,1};
Shell.sort(numbers);
System.out.println(Arrays.toString(numbers));
}
}
|
区别就是插入排序是按照顺序插入数的,希尔排序是按照顺序插入分好组的组内的数的。多了个分组。
7.3 时间复杂度
不好用大O法分析,用事后分析法,发现是插入排序的约千分之一。
8. 归并排序
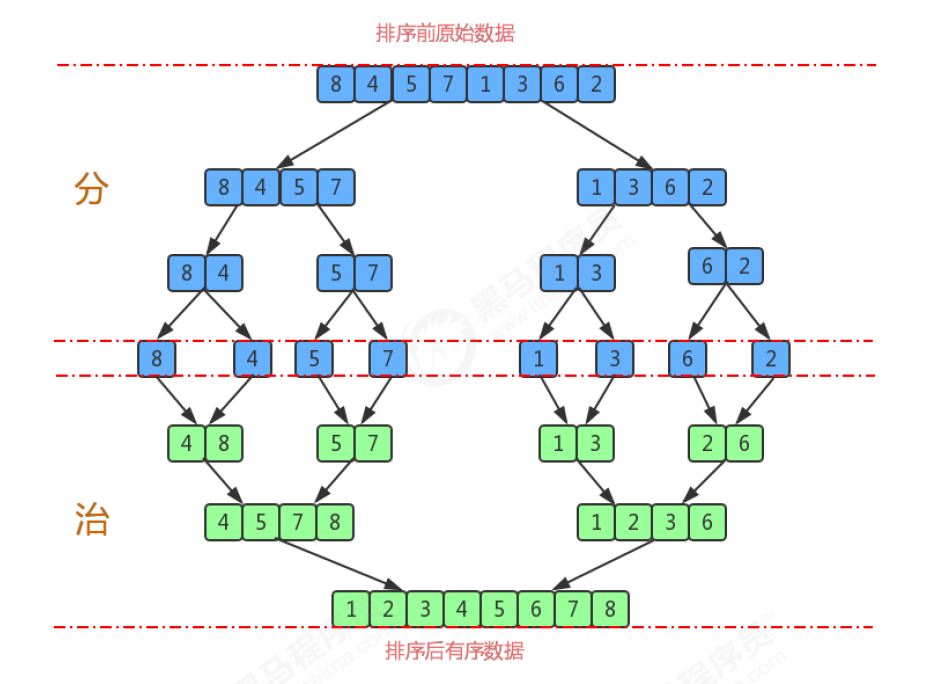
8.1 原理
- 尽可能的一组数据拆分成两个元素相等的子组,并对每一个子组继续拆分,直到拆分后的每个子组的元素个数是1为止。
- 将相邻的两个子组进行合并成一个有序的大组;
- 不断的重复步骤2,直到最终只有一个组为止。
8.2 代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
| package 归并排序;
public class Merge {
private static Integer[] assist;
public static void sort(Integer[] numbers) {
assist = new Integer[numbers.length];
int low = 0;
int high = numbers.length - 1;
sort(numbers, low, high);
}
public static void sort(Integer[] numbers, int low, int high) {
if (high <= low) {
return;
}
int mid = low + (high - low) / 2;
sort(numbers, low, mid);
sort(numbers, mid + 1, high);
merge(numbers, low, mid, high);
}
private static void merge(Integer[] numbers, int low, int mid, int high) {
int i = low;
int p1 = low;
int p2 = mid + 1;
while (p1 <= mid && p2 <= high) {
if (less(numbers[p1], numbers[p2])) {
assist[i] = numbers[p1];
i++;
p1++;
} else {
assist[i] = numbers[p2];
i++;
p2++;
}
}
while (p1 <= mid) {
assist[i] = numbers[p1];
i++;
p1++;
}
while (p2 <= high) {
assist[i] = numbers[p2];
i++;
p2++;
}
if (high + 1 - low >= 0) System.arraycopy(assist, low, numbers, low, high + 1 - low);
}
private static boolean less(Integer num1, Integer num2) {
return num1.compareTo(num2) < 0;
}
private static void exchange(Integer[] numbers, int i, int j) {
Integer tempValue = numbers[i];
numbers[i] = numbers[j];
numbers[j] = tempValue;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
| package 归并排序;
import java.util.Arrays;
public class test {
public static void main(String[] args) {
Integer[] numbers = {7,6,5,4,3,2,1};
Merge.sort(numbers);
System.out.println(Arrays.toString(numbers));
}
}
|
8.3 时间复杂度
时间复杂度是O(nlogn)。
9. 快速排序
9.1 原理
- 首先设定一个分界值,通过该分界值将数组分成左右两部分;
- 将大于或等于分界值的数据放到到数组右边,小于分界值的数据放到数组的左边。此时左边部分中各元素都小于或等于分界值,而右边部分中各元素都大于或等于分界值;
- 然后,左边和右边的数据可以独立排序。对于左侧的数组数据,又可以取一个分界值,将该部分数据分成左右两部分,同样在左边放置较小值,右边放置较大值。右侧的数组数据也可以做类似处理。
- 重复上述过程,可以看出,这是一个递归定义。通过递归将左侧部分排好序后,再递归排好右侧部分的顺序。当左侧和右侧两个部分的数据排完序后,整个数组的排序也就完成了。
9.2 代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
| package 快速排序;
public class quick {
public static void sort(Integer[] numbers) {
int low = 0;
int high = numbers.length - 1;
sort(numbers, low,high);
}
private static void sort(Integer[] numbers, int low, int high) {
if (high<=low){
return;
}
int partition = partition(numbers, low, high);
sort(numbers,low,partition-1);
sort(numbers,partition+1,high);
}
public static int partition(Integer[] numbers, int low, int high) {
Integer key=numbers[low];
int left=low;
int right=high+1;
while(true){
while(less(key,numbers[--right])){
if (right==low){
break;
}
}
while(less(numbers[++left],key)){
if (left==high){
break;
}
}
if (left>=right){
break;
}else{
exchange(numbers,left,right);
}
}
exchange(numbers,low,right);
return right;
}
private static boolean less(Integer num1, Integer num2) {
return num1.compareTo(num2) < 0;
}
private static void exchange(Integer[] numbers, int i, int j) {
Integer tempValue = numbers[i];
numbers[i] = numbers[j];
numbers[j] = tempValue;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
| package 快速排序;
import java.util.Arrays;
public class test {
public static void main(String[] args) {
Integer[] numbers = {7,6,5,4,3,2,1};
quick.sort(numbers);
System.out.println(Arrays.toString(numbers));
}
}
|
9.3 时间复杂度
最坏情况下:
时间复杂度是O(n2)。
平均情况下:
时间复杂度是O(nlogn)。
10. 排序函数的稳定性
| 排序名 |
稳定性 |
| 冒泡 |
稳定 |
| 选择 |
不稳定 |
| 插入 |
稳定 |
| 希尔 |
不稳定 |
| 归并 |
稳定 |
| 快速 |
不稳定 |









