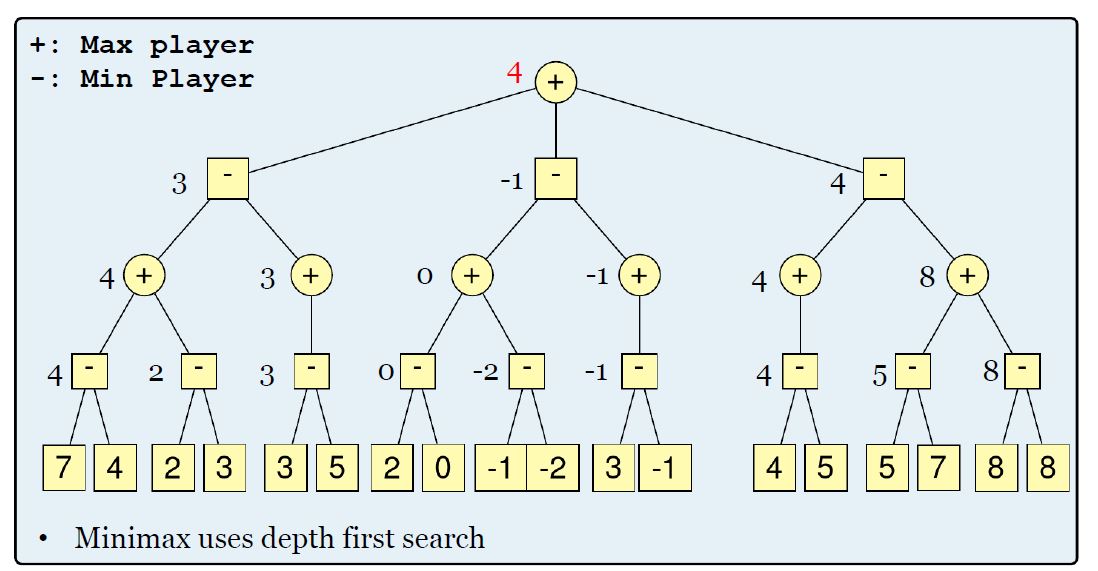
MiniMax算法

有两个玩家Max和Min，假设这两个玩家都铁分奴，不会假赛。
Min的战略
1. 想要分数尽可能地最低，最好是 $-\infty$ 。
2. 也必须考虑到Max会尽可能地让分数高，最坏是 $+\infty$ 。
3. Min的最佳策略是：选择使Max得分最高的移动时所得分数最小化的移动。
Max的战略和Min相反

MaxMin的游戏树

MiniMax算法的弊端

Alpha：到目前为止，在路径上找到的对于Max来说的最好（最高）值。

也就是说，对于Max， $\alpha$ 的值越高越好。

$\alpha$ 的值是实际结果的下限。
Beta：到目前为止，在路径上找到的对于Min来说的最好（最低）值。

也就是说，对于Min， $\beta$ 的值越高越好。

$\beta$ 的值是实际结果的上限。
a-b剪枝的伪代码是：

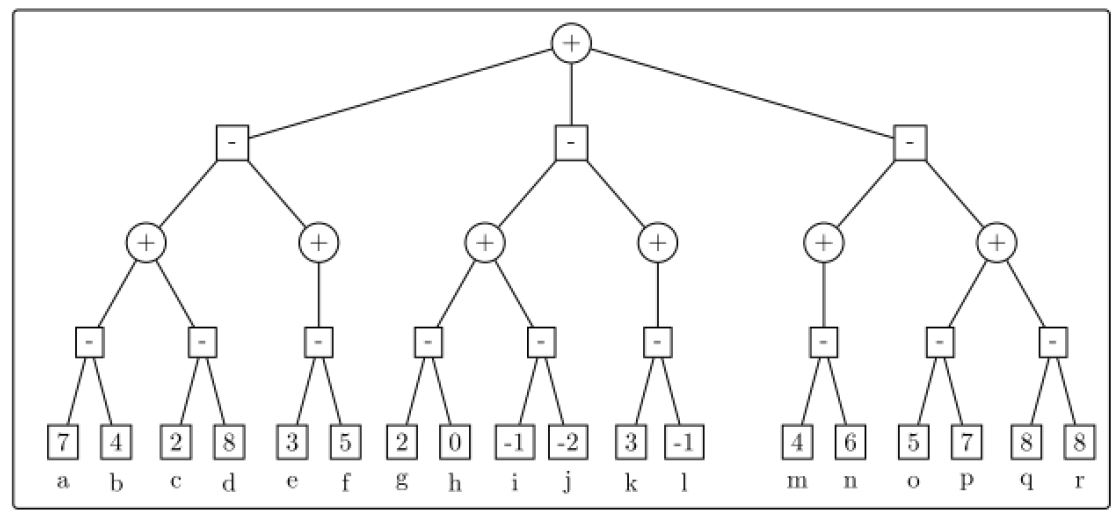
a-b剪枝的练习
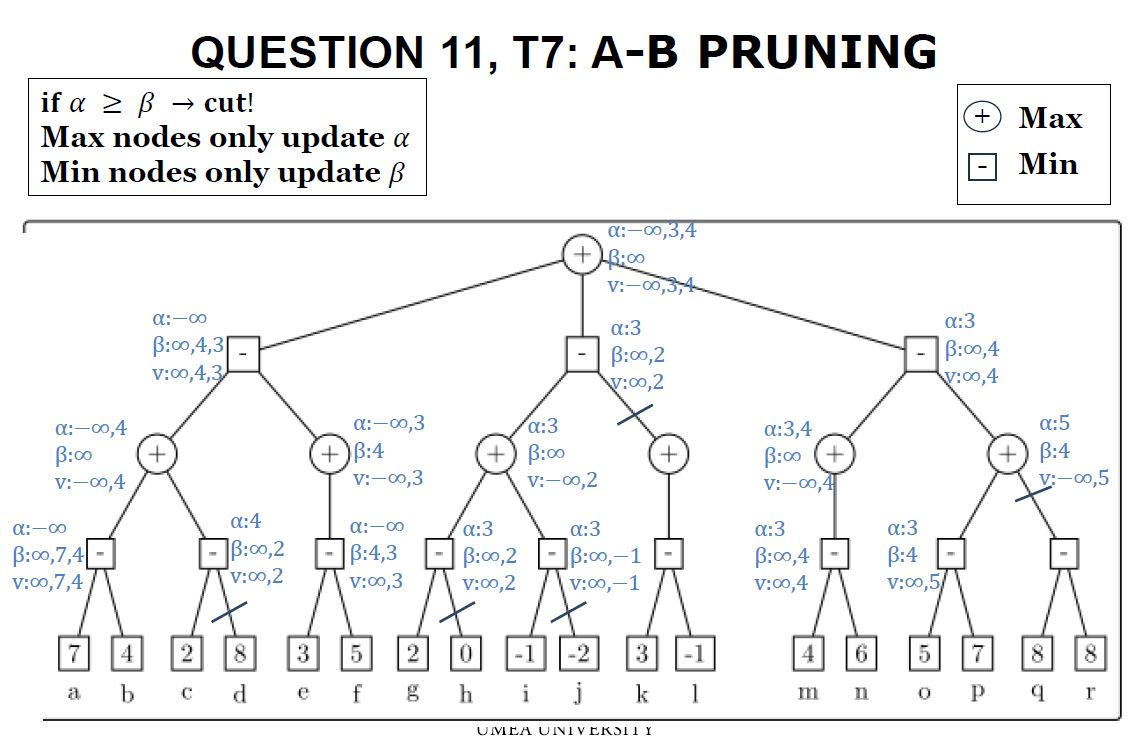
有如图所示的树，那么如何应用a-b剪枝呢？按照伪代码执行一遍：

答案：

MiniMax需要访问O( $b^d$ )个点。

Alpha Beta访问多少节点取决于检查移动的顺序。（比如A节点下面有a,b,c三个子节点，如果直接访问c几点，可以cut-off。但必须按照顺序访问a和b，这样就浪费时间了。）

我们可以使用特定领域的知识来实现合理的移动顺序。

对于国际象棋来说，有可能合理地接近最好的情况。

不能让Alpha Beta搜索整个游戏树（这对于国际象棋来说是不现实的），我们应该希望中断搜索并返回一个启发式评估。
一个简单的方法:设置搜索深度（需要确保，在当前深度下多搜索一层也可以在时间限制内完成。）
更有鲁棒性的方法：使用IDS迭代深度搜索。
1. 从深度1开始，使用ab算法，返回一个结果，并储存。然后从深度2开始，循环。
2. 当时间到了，返回最深次完成的移动结果。
3. 额外的：人工的修改移动顺序。
4. 仅为搜索呈指数增长的树添加固定时间

增加动态行棋排序方案，如先试图采用以前走过的最好行棋，可能让我们非常接近理论极限。以前的行棋可能是上一步棋—— 面临同样的棋局威胁—— 也可能来自当前行棋的上一次搜索过程。

从当前行棋获得信息的一种方法是迭代深入搜索。首先，搜索一层并记录最好行棋路径。接着搜索更深一层，此时使用记录的路径来导引行棋排序。最好行棋称为绝招，先走绝招称为绝招启发式。